В работе [1] при рассмотрении вопроса оптимизации территориального размещения малых электростанций (ЭС) была получена зависимость для определения радиуса эффективности электростанции Rэфф – расстояния, на котором энергообеспечение локального потребителя за счет уже существующей поблизости ЭС будет дешевле строительства новой ЭС на месте потребления:
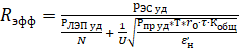(1)
и зависимость для расчета оптимального сечения проводов ЛЭП:
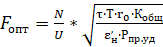(2)
где Rэфф – радиус эффективности, км
РЭС уд – удельная стоимость строительства ЭС, долл/Вт
РЛЭП уд - удельная стоимость строительства ЛЭП, долл/км.
N – мощность, Вт
U – напряжение ЛЭП, В
Ппри уд – удельная стоимость провода, долл/км·мм2
Т – рассматриваемый период времени, час
r0 - удельное сопротивление провода, Ом*мм2/км
τ - тариф на электроэнергию, долл/Вт·ч
Кобщ =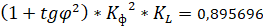 
tgφ - коэффициент реактивной мощности (0,6)
Кф² - коэффициент заполнения графика:
Kф² = (1 + 2Кз)/3K
Кз - коэффициент заполнения графика (при отсутствии данных о форме графика нагрузки обычно принимается значение - 0,3; тогда: Kф² = 1,78)
КL - коэффициент, учитывающий распределённость нагрузки по линии (0,37 - для линии с распределённой нагрузкой)
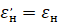+0,03 = 0,15
εн – нормативный коэффициент эффективности использования капитальных вложений (в энергетике – εн = 0.12).
В формулах (1) и (2) мощность N – независимая переменная, а все остальные параметры, кроме напряжения ЛЭП U, однозначно определяются конкретными условиями решаемой задачи. В отличие от них, напряжение U в этих формулах должно назначаться произвольно, или по нормам [2], предназначенным для мощностей, существенно превышающих мощности малых ЭС.
В настоящей статье рассматривается вопрос технико-экономического обоснования выбора U для ЛЭП малых ЭС с использованием критерия минимизации общих приведенных затрат на строительство и эксплуатацию ЛЭП. Такие приведенные затраты состоят из стоимости строительства ЛЭП с ежегодными эксплуатационными издержками (первое слагаемое в формуле (3)) и ежегодными потерями электроэнергии в ЛЭП (второе слагаемое в формуле 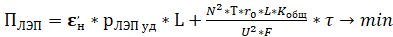(3)).
(3)
Удельная стоимость ЛЭП в формуле (3) может быть представлена в виде функции U (рис. 1), как аппроксимация[1] современных стоимостей ЛЭП [3, 4]:
РЛЭП уд = 4015,5*U0,1603 (4)
где 4015,5 – размерный коэффициент =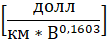 
Подставив (4) в (3), и дифференцируя, будем иметь:
Подставив (4) в (3), и дифференцируя, будем иметь:
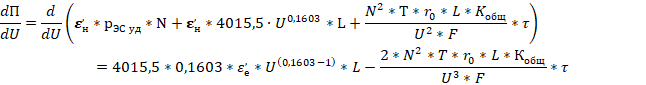
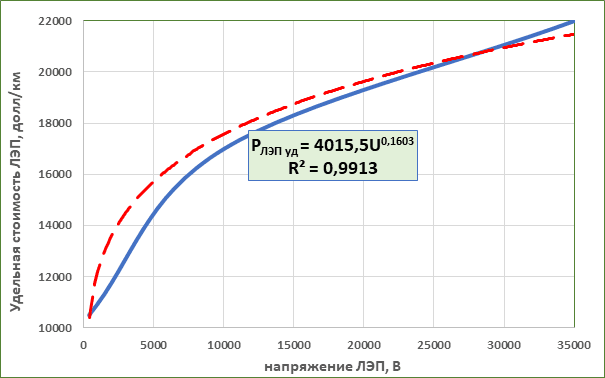
Рис. 1. РЛэп.уд = f(U)
Откуда, сокращай на L и приравнивания нулю, после упрощения получим уравнение для оптимального значения мощности ЛЭП, U:
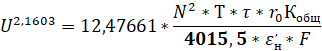(5)
Подставив в (5) значение Fопт из (2), получим:
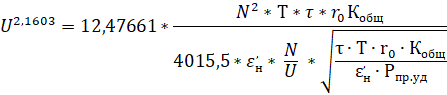
или:
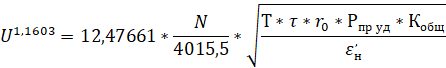
Откуда:
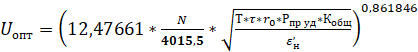(6)
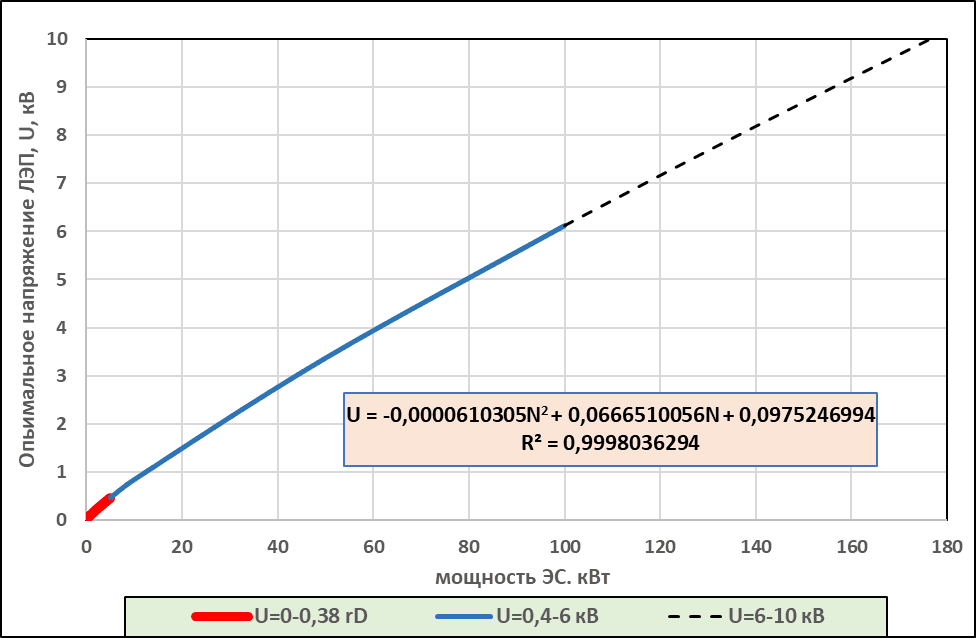
Рис. 2. Оптимальные диапазоны напряжения ЛЭП, U для разных мощностей ЭС, N
Используя (6), можно рассчитать оптимальные значения напряжений, U для различных значений мощности N. Такие расчеты для значений входящих в нее параметров, приведенных в таблице 1[2], показаны в таблице 2 и на рис. 2.
Таблица 1
|
|
0,15 |
б/р |
|
РЭС.уд = |
3 |
долл/Вт |
|
Т = |
8760 |
час/год |
|
Кобщ = |
0,895696 |
б/р |
|
τ = |
0,000145 |
долл/Втч |
|
r0 = |
28 |
Ом*мм2/км |
|
Рпр.уд = |
30 |
долл/км*мм2 |
=Таблица 2
Оптимальные значения напряжения ЛЭП, Uопт, для разных N
|
Диапазон N, кВт |
0 - 4 |
4 - 100 |
100 - 180 |
|
Uопт, В |
380 |
6000 |
10000 |
Интересно сравнить сечения проводов в различных диапазонах оптимальных значений напряжения ЛЭП. Результаты таких расчетов по формуле (2) для оптимальных диапазонов U показаны на рис. 3.
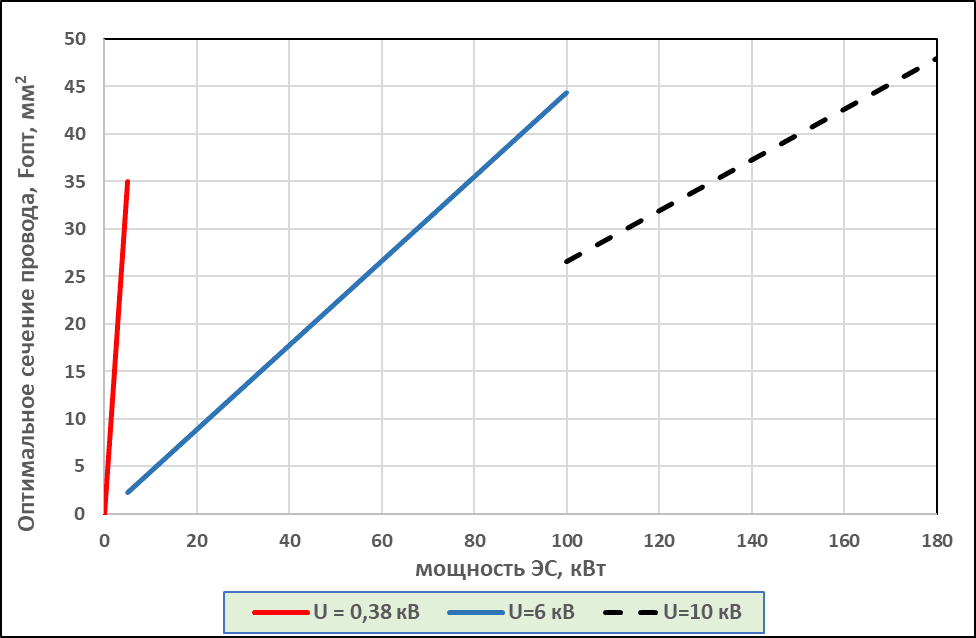
Рис. 3. Fопт = f(N) при разных U
Также, используя (1), можно рассчитать уточненное значение радиуса эффективности ЭС, Rэфф для оптимальных диапазонов U (табл.). Результаты таких расчетов Rэфф показаны на рис. 4.
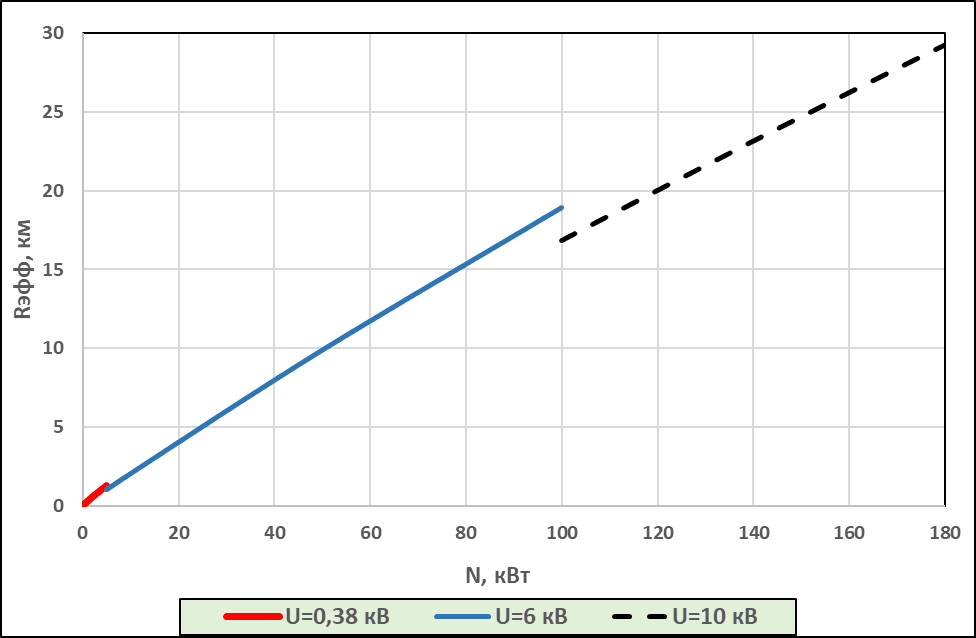
Рис. 4. Rэфф = f(N) при различных U и РЛЭП уд
Таким образом, мы полностью решили задачу, поставленную в работе [1], продолжением которой является настоящая статья: рассчитать радиус эффективности Rэфф для потребителя мощностью N, на границе которого приведенная стоимость строительства ЛЭП от уже существующей ЭС равна приведенной стоимости строительства новой ЭС непосредственно у потребителя. Одновременно были решены вопросы оптимизации сечения проводов ЛЭП и ее напряжения.
Для того, чтобы убедиться в правильности решения этой задачи, в заключение, используя все полученные выше результаты, рассчитаем приведенные стоимости этих двух сравниваемых вариантов.
В первом варианте удельная стоимость, в соответствии с формулой (1) будет равна:
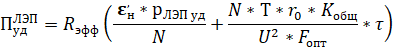(7)
Результаты расчетов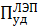 
, выполненных по зависимости (7), для тех же значений параметров, что и ранее, приведены в таблице 3.
Таблица 3
|
N, кВт |
3,970595 |
97,57118 |
176,4951 |
|
U, В |
380 |
6000 |
10000 |
|
N, Вт |
3970,595 |
97571,18 |
176495,1 |
|
Fопт, мм2 |
27,80104 |
43,26726 |
46,95932 |
|
РЛЭП уд |
10500 |
14500 |
17000 |
|
Rэфф, км |
1,050975 |
18,5285 |
28,76265 |
|
Пуд, долл/Вт |
0,45 |
0,45 |
0,45 |
Во втором варианте – строительства ЭС, приведённая стоимость определяется выражением [1]:
,
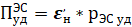в соответствие с которым, она для всех рассматриваемых нами случаев, для которых Рэс уд = 3 долл/Вт = const, будет одна и та же, равная:
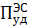=0,15*3 = 0,45
То есть, выполненная оптимизация сечения проводов ЛЭП, F и ее напряжения, U, для соответствующих значений Rэфф обеспечивает равенство:
ВЫВОДЫ
Предложенный в статье метод позволяет рассчитать оптимальное напряжение ЛЭП, соответствующее мощности потребителя и выделить диапазоны мощности, соответствующие используемым сегодня на практике напряжениям ЛЭП: 0,38, 6 и 19 кВ.
При использовании одновременно с этом метода оптимизации сечения проводов ЛЭП [1], это дает возможность оптимизировать территориальное размещение малых электростанций, при котором каждая из них располагается от потребителя на расстоянии, меньшем соответствующего радиуса эффективности.
[1] Для такой аппроксимации не требуется особая точность, так как она необходима только для выделения соответствующих диапазонов мощности для оптимальных значений U, из которых реально используется на практике всего несколько значений: 0,38, 6, 10 …кВ.
[2] Также, как и в [1] все расчеты в настоящей статье сделаны для конкретных параметров малых ГЭС, но вся методика может успешно применяться и для любых других ЭС.
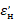.png&w=640&q=75)
