Формирование Глобальной информационной сети, являющееся одной из основных тенденций развития мировой экономики [14, c.16], возможно при дополнении наземного сектора сетей 5G космической составляющей в виде Глобальных навигационных спутниковых сетей (ГНСС). Подтверждает сказанное российский проект ESIM (Earth stations in motion) [15], который в совокупности со спутниками HTS (High Throughput Satellite) должен обеспечивать широкополосным доступом мобильных абонентов, перемещающихся на высокоскоростном на наземном, морском или воздушном транспорте. Одним из основных вопросов для систем, подобных ESIM, является, как показано в [13, 15], синхронизация по времени наземного и космического сегментов. При этом задержка в передаче сигналов для сетей 5G не должна превышать 10 мс для абонентов, передвигающихся с медленной скоростью, например, пешеходов, и 1 мс – в случае перемещения на высокой скорости. В известных в настоящее время спутниковых системах данный параметр сильно отличается в большую сторону [15]. Уменьшение данной величины достигается путем предварительных расчетов положений спутника на основе справочной информации с занесением данных в соответствующий альманах (базу данных) [6]. При этом на величину задержки основное влияние (порядка 50 % от величины погрешности) оказывает атмосфера Земли [17], т.е. ее ионосферный и тропосферный слои. Тропосферная задержка в распространении радиоволны, обусловленная содержанием кислорода и водяных паров, вызывающих явление дифракции электромагнитной волны [6, c.121], относится к оцениваемым параметрам, что позволяет для каждого положения спутника определить его заранее по полученной бесплатно от международных служб дополнительной информации (цифровые карты погоды, параметры вращения Земли и т.д.). В результате обеспечивается точность вычисления зенитной задержки порядка 90 % от измеренной. Однако при наклонных радиотрассах и малых углах возвышения вследствие существенных различий вдоль трассы в содержании воды в атмосфере (облака, осадки), так и свойств подстилающей поверхности измеренная величина влажной составляющей тропосферной задержки изменяется случайным образом в интервале от 20 см до 20-28 м [8, с. 243; 9]. В связи с этим при проведении предварительного моделирования возникает вопрос снизить данную ошибку путем выбора соответствующей модели структуры тропосферы.
Цель доклада – оценка величины тропосферной задержки сигнала при использовании различных имитационных моделей.
Решаемая задача
Анализ влияния выбранной модели тропосферной модели на величину наклонной тропосферной задержки.
Используемые методы
При проведении исследований используем методы космической геодезии и статистической метеорологии [8].
Результаты исследований
В настоящее время для вычисления поправок за влияние тропосферы используются несколько моделей тропосферной задержки сигнала [3, 4, 6, 10-12, 16], например, Хопфилда, Саастамойнена, Блэка, Нейвилла, GCAT, MOPS и др. Как показал выполненный анализ литературы, моделирование тропосферной задержки может осуществляться с помощью двух различных подходов, основанных на моделировании либо распределения индекса преломления по высоте, либо величин метеорологических параметров, т.е. фактически зависят от способа получения информации о метеорологических параметрах. Результаты проведенных исследований по влиянию источника информации приведены на рис.1 и 2.
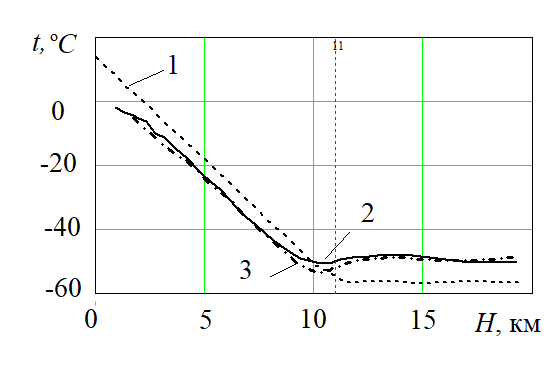
Рис. 1. Зависимость температуры от высоты над поверхностью Земли:
1 – по модели стандартной тропосферы;
2 – по данным измерений радиозондов;
3 – по статистическим метеорологическим данным
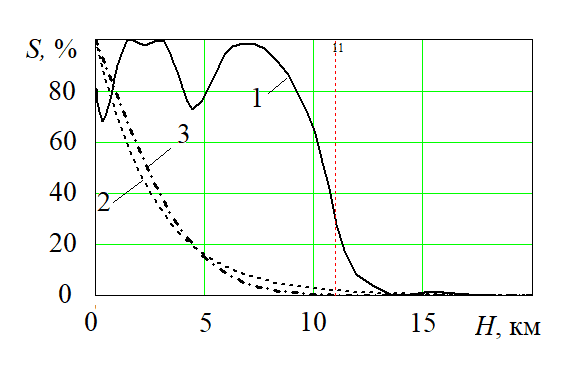
Рис. 2. Зависимость величины относительной влажности в атмосфере от высоты:
1 ‑ по данным измерений радиозондов;
2 – по модели Ганна;
3 – по модели Зюрцига-Хргиана
На данных рисунках вертикальная штриховая линия обозначает верхнюю границы тропосферы в соответствии с моделью стандартной тропосферы. Несложно заметить, что в пределах тропосферы для моделирования вертикального профиля температуры возможно использование модели стандартной тропосферы. В то же время эмпирические модели вертикального профиля влажности не учитывают наличия в атмосфере аномалий высотного профиля влажности. Вследствие этого они дают большие погрешности при построении вертикального профиля влажности. Вертикальные профили температуры и влажности, полученные с использованием статистических данных, ненамного отличаются от измеренных значений. В связи с этим статистические модели могут быть использованы для нахождения вертикального профиля индекса преломления тропосферы. В связи с этим для нахождения влажной составляющей тропосферной задержки по данным радиоизмерений используется второй вариант из описанных выше подходов, причем метеорологические параметры вдоль трассы обычно находятся в результате статистической обработки метеорологических данных по всему Земному шару за длительный (порядка 10-20 лет) период наблюдений [8, с.267]. Для сухой составляющей тропосферной задержки, зависящей от содержания кислорода в воздухе, наибольшее распространение получили модели Саастамойнена и Хопфилд [8, с.254]. Данные модели используют только наземные оперативные метеорологические данные в месте расположения приемника Глобальной навигационной спутниковой системы и не учитывают фактические данные о вертикальных профилях атмосферы, поскольку базируются на модели стандартной тропосферы.
Дальнейшим развитием данных моделей является модель тропосферы GPT2, предложенная в [1] и подробно описанная в [2, 7]. Модель предназначена для больших по площади территорий, различающихся климатическими условиями. В ее основе для описания сухой составляющей тропосферной задержки применяется модель Саастамойнена, а для влажной – приближения Каллахана для распределения давления водяных паров по высоте. В качестве информации о метеорологических условиях на уровне моря используются статистические данные, накопленные на исследуемом участке местности за длительный промежуток времени (порядка 20 лет). Модернизацией модели GPT2 является модель MOPS [11]. Её особенностью является применение только на территории Европы. Вследствие записи информации по широтным поясам кратностью , сокращается время вычислений, что позволяет использовать данную модель в автономных приемниках без необходимости использования специального оборудования или поддержания связи с ближайшей метеорологической станицей. Модель определена для углов видимости спутника вплоть до над уровнем горизонта.
В обеих моделях вычисляется только зенитная составляющая тропосферной задержки. Для вычисления наклонной тропосферной задержки для обеих составляющих (сухой и влажной) применяются функции отображения (мапирующие функции). Величины данных функций зависят от модели распространения лучей в атмосфере и связаны с широтой, высотой и временем года, а также углом возвышения траектории.
Вычислительные затраты функций отображения можно существенным образом сократить при увеличении погрешности вычислений не более чем на 5 % [8], если вместо двух отдельных функций отображения применять одну глобальную. Указанная замена возможна в предположении, что состояние тропосферы соответствует обычному для данной местности, а нерегулярностями (тайфунами, смерчами и т.д.) можно пренебречь.
Как показано в [8, с.265], неоднородность атмосферы в горизонтальном направлении может быть учтена, если известна информация о величинах компонент горизонтального градиента тропосферной задержки в направлениях север-юг и восток-запад. Там же показано, что градиентная часть тропосферной задержки обычно не превышает 3 см. Однако для обеспечения задержек менее 1 мс данная составляющая должна быть учтена. С этой целью модель стандартной тропосферы, используемая в модели Саастамойнена, дополняется еще двум: градиентной моделью и турбулентной моделью, учитывающей корреляцию значений влажной задержки в направлениях север-юг и восток-запад. При этом учет градиентной модели позволяет снизить погрешность вычислений на 3-7 мм, а турбулентной – еще на 1-5 мм.
Следует отметить, что последняя модификация модели GPT2 – GPT3 [7] в настоящее время позволяет учесть градиентные изменения атмосферы, что делает ее наиболее точной по сравнению с остальными известными.
Обсуждение результатов исследований
Выполненный анализ используемых в настоящее время методов определения наклонной тропосферной задержки показал, что
- использование статистической модели обеспечивает получение составляющих тропосферной задержки практически с той же точностью, что и по измеренным вдоль радиотрассы метеопараметрам;
- наибольшее расхождение между полученными результатами наблюдается для влажной составляющей наклонной тропосферной задержки. Это вполне объяснимо случайным характером изменения влажности вдоль наклонной трассы распространения радиоволны;
- суммарная оценка тропосферной задержки как зенитной, так и наклонной, хорошо согласуется с результатами, полученными с использованием более грубых моделей (Саастамойнена и Хопфилд). Однако в этом случае расхождение составляет уже не миллиметры, как для зенитной задержки, а несколько (порядка трех) метров. Разница в получаемых результатах обусловлена отказом от учета горизонтальных неоднородностей влажности;
- наиболее полной статистической погодной картой, учитывающей не только распределение водяных паров по высотному профилю, но и градиент их изменения по широте, является программный комплекс GPT3, разработанный Австрийским департаментом Геодезии и геоинформатики и находящийся в свободном доступе. Проведенные исследования показали, что использование статистической погодной карты обеспечивает получение составляющих тропосферной задержки практически с той же точностью, что и по измеренным вдоль радиотрассы метеопараметрам. В качестве ограничения выступает размерность наземной сетки, в которой представлены результаты измерений (либо 5°×5°, либо 1°×1°).
Выводы
Выполненный анализ известных моделей структуры тропосферы показал, что наиболее полной статистической погодной картой, учитывающей не только распределение водяных паров по высотному профилю, но и градиент их изменения по широте, является программный комплекс GPT3, разработанный Австрийским департаментом Геодезии и геоинформатики и находящийся в свободном доступе. Расчеты, проводимые с его использованием, позволяют существенным образом снизить погрешность вычислений, а, следовательно, и точность определения координат мобильных абонентов, перемещающихся в наземном секторе с высокими скоростями.

.png&w=640&q=75)