В монографии [1] качественно рассмотрено взаимодействие возмущений различной природы. В том числе взаимодействие возмущений плотности (акустических) с вихревыми. Такие процессы могут быть важны с точки зрения теории турбулентности вязких течений. Предполагается, что течение в канале подчиняется уравнениям Навье-Стокса.
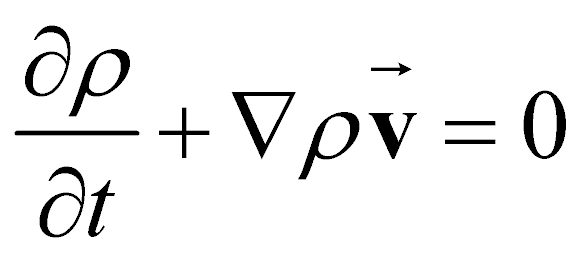
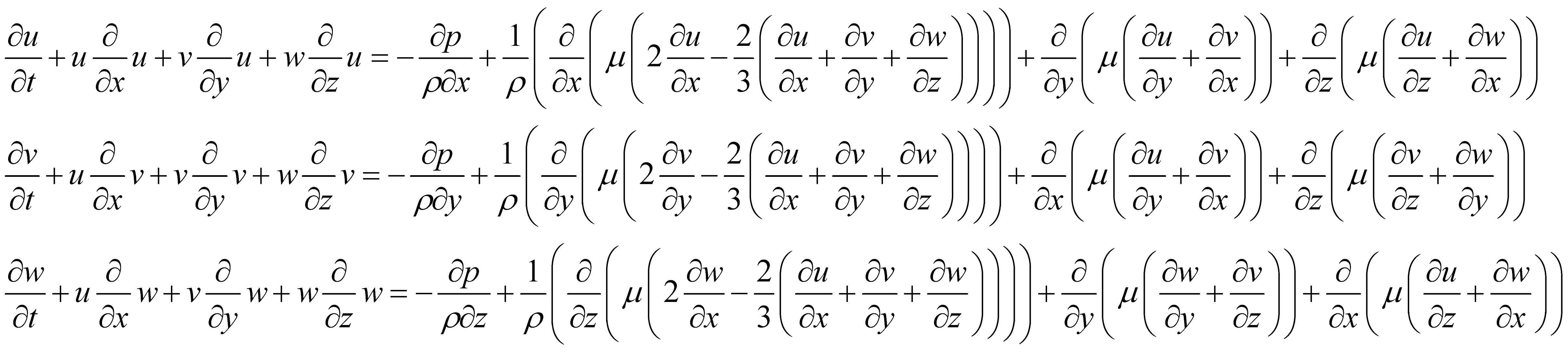
Далее предполагается, что вязкость практически постоянна. Считаем, что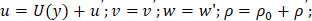 
Для выявления эффективности подобных взаимодействий преобразуем линеаризованные уравнения Навье-Стокса в канале, так, чтобы акустические и вязкие возмущения были выделены в явном виде.
Линеаризованные уравнения приводятся к виду: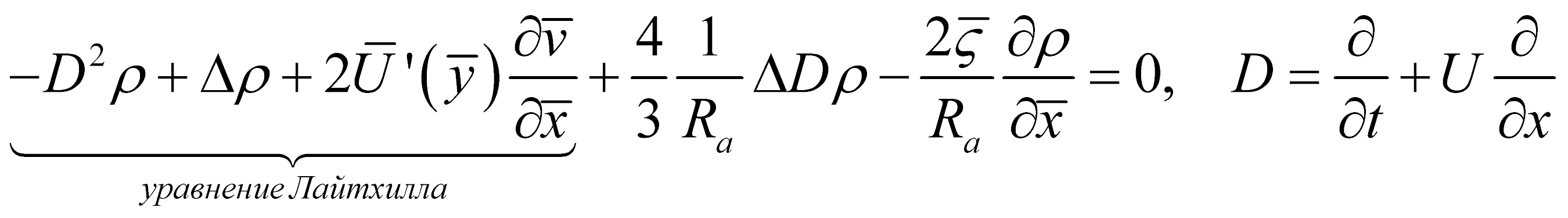
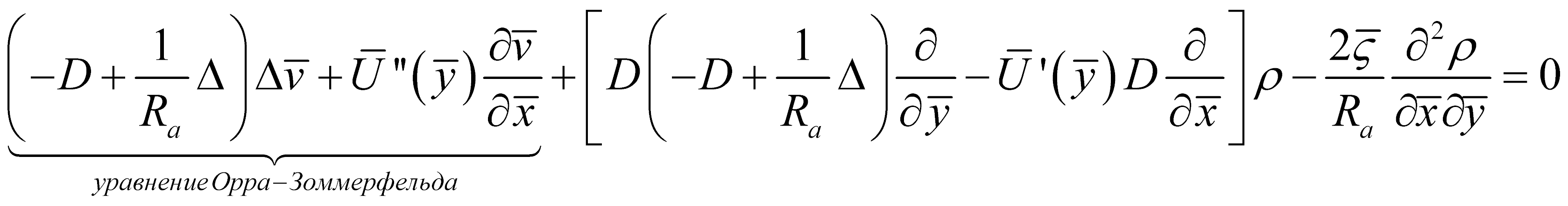
Здесь уравнения представлены в такой форме, что выделенная часть этих уравнений совпадает с известными уравнениями акустики и теории устойчивости. В то время как правая часть может быть проинтерпретирована как взаимодействие акустических возмущений (возмущений плотности) с возмущениями вязкими (вихревыми). К этим уравнениям необходимо добавить граничные условия на стенках канала
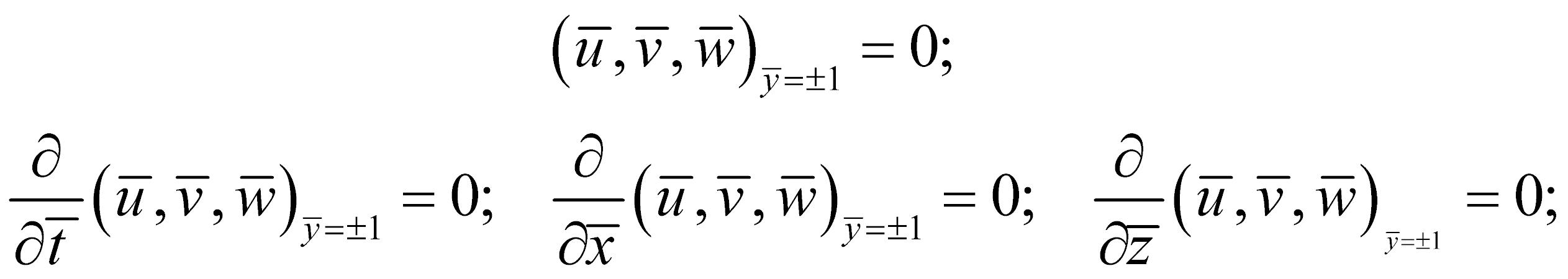
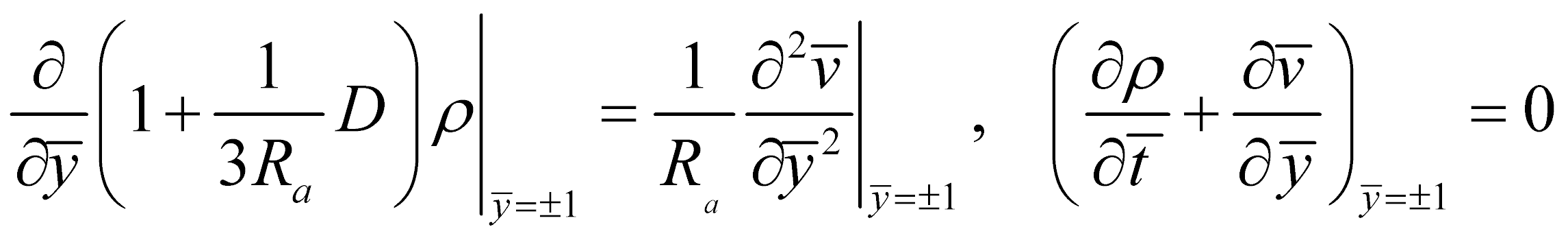
Полученная система линейных уравнений при нулевой скорости на границе канала и параболическом профиле фоновой скорости соответствует некоторой спектральной задаче, если искать решение в виде бегущих волн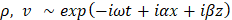 
. Далее рассматривается плоская постановка задачи: . Решение этой спектральной задачи отыскивается численно. Для этого дифференциальные уравнения приводятся к матричным с помощью разностной схемы.
Для построения разностной схемы воспользуемся следующим методом:
1. Так как у меняется от -1 до 1, интервал поделён на 2n+1 точку с шагом сетки 
;
2. Рассматриваем интеграл данных формул
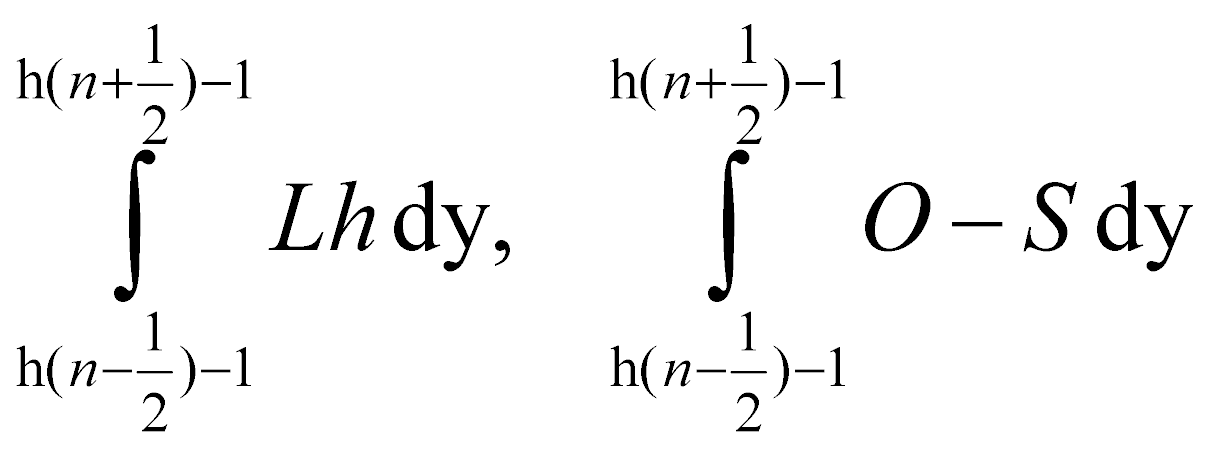
3. Полученные интегралы вычисляем методом трапеций, оставшиеся производные заменяем на центральные разности:
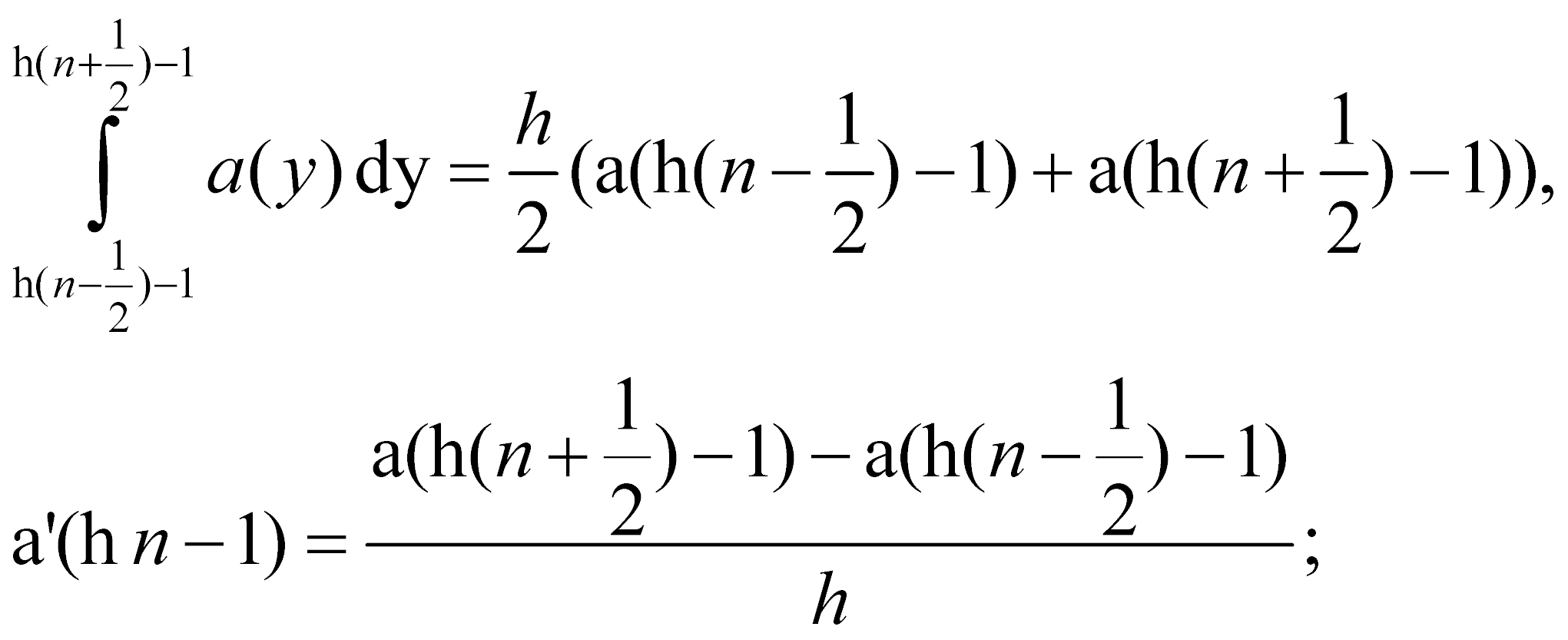
4. Функции, полученные в половинных точках, заменяем на среднее значение в соседних точка
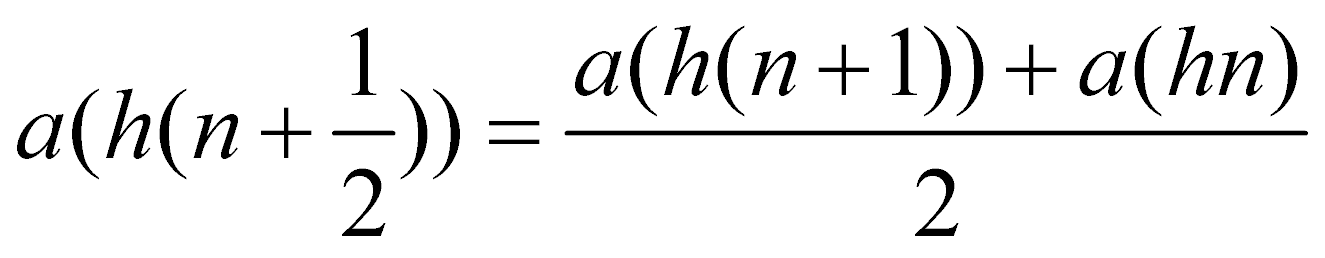
Для того, чтобы решать задачу на собственные значения ω, необходимо привести эту матрицу к задаче вида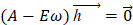 
, 
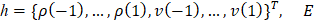– единичная матрица, и преобразовать эту матрицу в блочную следующим образом. Представим исходную матрицу в виде
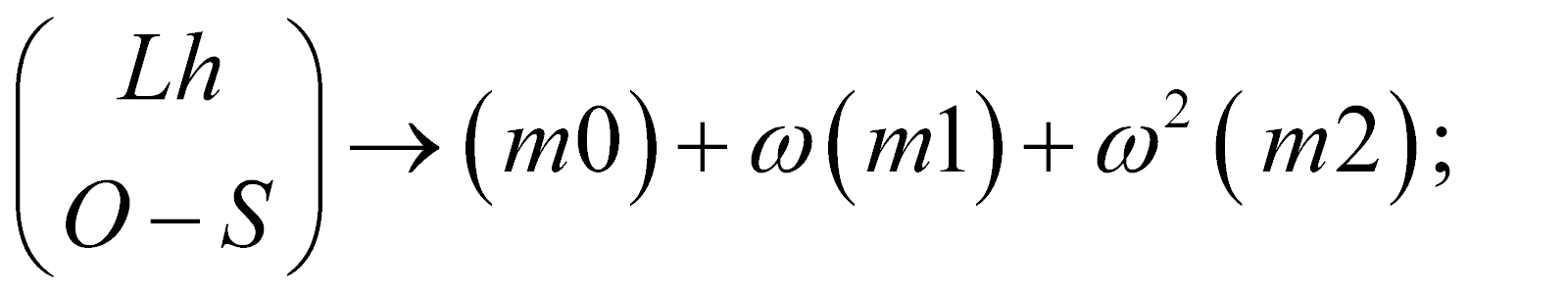Здесь Lh часть матричных членов, которые получаются из уравнения Лайтхилла, через O-S обозначена часть членов, которая получается из уравнения Орра-Зоммерфельда.
Тогда задача сведется к следующей:
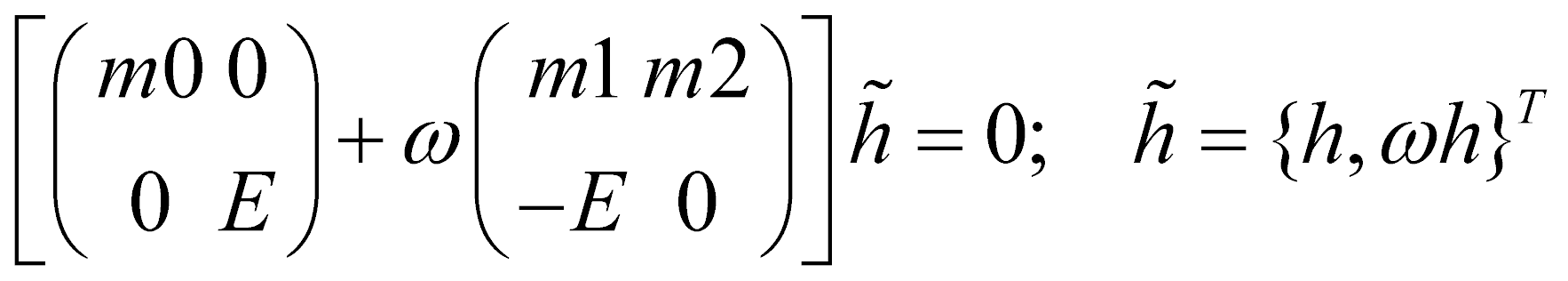
Здесь m0, m1, m2, E – матрицы размером 2(2n+1)×2(2n+1). Численно эта задача решалась с помощью пакета MATHEMATICA [2].
Для проверки работоспособности данного метода, полученные результаты при достаточно больших n (~200) были сравнены с результатами монографии [3] для уравнения Орра-Зоммерфельда. На графиках приведены собственные значения на мнимой и действительной оси (рис. 1 и 2). Вид картины и значения мод совпадают с теми, что и в [3]. Из этого можно сделать вывод, что рассмотренный выше метод можно использовать для решения этой задачи.
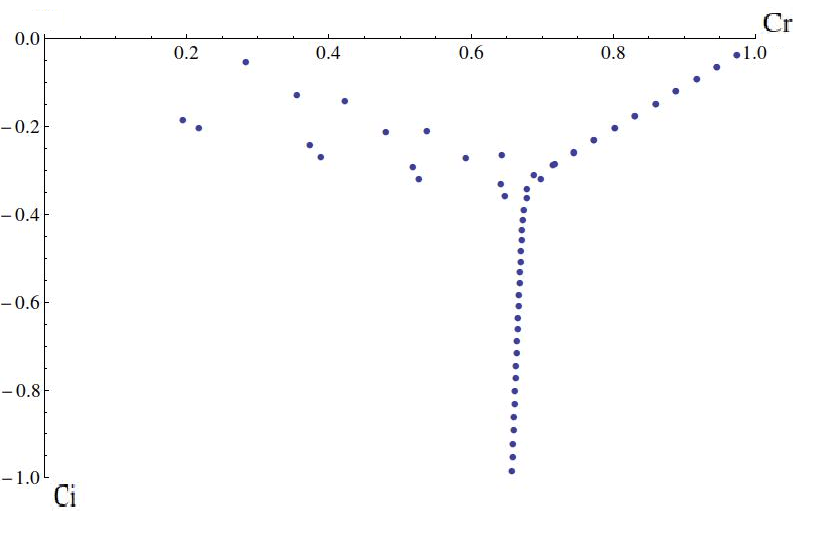
Рис. 1. Собственные числа исходной системы уравнений в канале
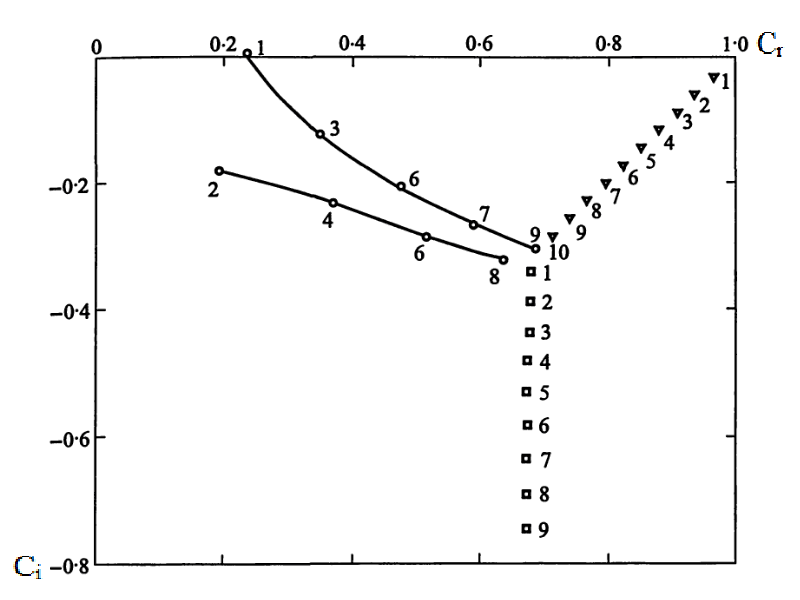
Рис. 2. Собственные числа мод в канале [3]
Получено поле скоростей для наименее затухающей моды и линии уровня завихренности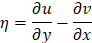 
(рис. 4) в канале. На графиках отчетливо видно распределение вихрей и их вид в канале.
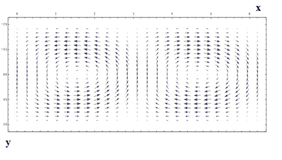
Рис. 3. Поле скорости вихревой моды в канале
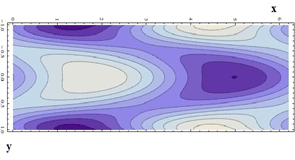
Рис. 4. Линии уровня завихренности вихревой моды в канале
Для сравнения приведем результаты приведенные в монографии [4] (см. рис. 5).
Рис. 5. Структура пафов в канале [4]
На рис. 3 и рис. 4 видна периодичность и характерная форма пафа, которая выявлена при визуализации вязко-акустических мод. Подобная структура обнаруживается в численном эксперименте [4]. Можно предположить, что рассмотренные моды легко теряют устойчивость (как в тороидальных вихрях, образованных акустическим полем [5, 6]) и приобретают структуру близкую к турбулентной. Таким образом, переход в каналах может осуществляться за счет развития неустойчивости вязко-акустических тороидальных мод даже при не очень больших числах Маха основного течения при наличии поперечной неоднородности потока в канале.
