Введение. Для конфликтно управляемой динамической системы, описываемой обыкновенным векторным линейным уравнением, в игровой постановке, рассматривается задача об оптимальном управлении по принципу обратной связи, при неполной информации о динамической помехе [1-9] и при запаздывающей информации о значениях фазовой переменной, характеризующей текущее состояние системы. Критерий качества процесса управления γ
задается в виде функционала от движения объекта и реализаций управляющих воздействий и помех. Задача на минимакс-максимин критерия качества формализуется в виде антагонистической дифференциальной игры двух лиц в классе чистых позиционных стратегий в рамках концепции дифференциальных игр, разработанной в Свердловске (ныне Екатеринбурге) в школе академика Н.Н. Красовского. Цель работы – обоснование понятия запаздывания по времени информации, поступающей в орган управления.
Динамический объект. Рассматривается объект, движение которого описывается обыкновенным векторным дифференциальным уравнением
x=Α(t)x+Β(t)u+C(t)υ, t0 ≤ t ≤ ϑ. (1)
Здесь x – n -мерный фазовый вектор управляемого объекта; t – время, моменты времени t0 и ϑ зафиксированы; u – r-мерный вектор управления, υ – s-мерный вектор помехи, стесненные условиями
u ∈ P, υ ∈ Q,
где P и Q – компакты [9].
Критерий качества. Для процесса, включающего в себя на отрезке времени [t0, ϑ]:
1. Движение
x[t0[⋅]ϑ]= {x[t], t0 ≤ t ≤ϑ}
2. Реализацию управления
u[t0[⋅]ϑ) = {u[t] ∈ P, t0 ≤ t ≤ ϑ}
3. Реализацию помехи
υ[t0[⋅]ϑ) = {υ[t] ∈ Q, t0 ≤ t ≤ ϑ}
будем рассматривать критерий качества процесса управления [2-6, 9] γ следующего вида
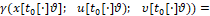
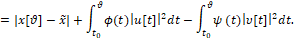(2)
Здесь x – некоторый фиксированный n-мерный вектор.
В (2) ϕ(t) и ψ(t) суть заданные кусочно-непрерывные функции времени t, ϕ(t)≤α, ψ(t)≤β,
, где α>0, β>0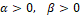
– заданные числа. Содержательно интегральные члены в (2) определяют затраты энергии на выработку управляющих воздействий и помех.
Задача. Рассмотрим задачу для x-объекта (1) о выборе управлений u и помех υ соответственно, минимизирующих и максимизирующих критерий качества γ (2). При этом задача решается при неполной информации о действующих динамических помехах и, что существенно, при запаздывающей по времени t информации о состояниях x [t] объекта (1) в схеме управления по принципу обратной связи [3].
Информационный образ. Текущую информацию при t≥t0+h, где h>0 величина запаздывания, будем использовать в виде n-мерного вектора x*[t], где
x*[t]=x[t-h] , t≥t0+h. (3)
Величина (3) и будет являться информационным образом для построения оптимальной стратегии
u0t,x*,ε, t≥t0+h,ε>0. (4)
с использованием конструкции экстремального сдвига из работы авторов [4].
До момента времени t0+h управление u[t0[⋅]t0+h)= {u[t]∈P, t0≤t≤t0+h} определяется лишь информацией об x0* = x*[t0]. Начиная с момента времени t0+h, управление u[t0+h[⋅]t) = {u[τ]∈P, t0+h≤τ≤t} определяется информацией об x*[t] (3). При этом, несмотря на содержательный смысл величин x0* и x*[t], вытекающий из (3), не будем требовать, чтобы обязательно выполнялось равенство
x*[t0+h]=x0*.
При этом при t ∈ [t0+h, ϑ] предполагается возможным запоминание истории x*[t0[⋅]t] = {x*[τ], t0+h≤τ≤t} и реализации выработанного управления u[t0[⋅]t) = {u[τ] ∈ P, t0<τ≤t}.
Запаздывание информации. Целью работы является обоснование используемого здесь понятия запаздывания информации. Величина h не есть, вообще говоря, только время запаздывания подачи информации о состояниях x[τ] в орган управления U. Величина h – это суммарное время, которое складывается из времени h* запаздывания подачи информации в ЭВМ в орган управления, из времени h* на подсчет в ЭВМ значения u[t] управляющего воздействия и из времени h передачи u[t] на x-объект. Итак,
h=h*+h*+h.
Используя схему соответствующих конструкций из работ авторов [3-5], получаем, что справедливо следующее утверждение.
Теорема. Оптимальная позиционная стратегия управления (4) для объекта (1) и показателя качества процесса (2) существует. Она строится конструктивно методом экстремального сдвига [4].
.png&w=640&q=75)
