Геометрия – одна из древнейших наук, занимающаяся изучением свойств геометрических фигур на плоскости и в пространстве. Современным школьникам приходится уделять очень много времени обучению и выполнению домашних заданий, ведь почти каждая геометрическая задача нестандартна, особенно задачи на доказательство.
В теме «Четырехугольники» проблему с доказательствами поможет решить использование теоремы Вариньона. В данной статье приведено доказательство теоремы Пьера Вариньона и некоторых следствий из неё с использованием авторских чертежей, созданных в программе GeoGebra, а также рассмотрены несколько задач, решенных традиционным способом и с помощью применения вышеуказанной теоремы.
Взявшись за данную статью, автор столкнулась с тем, что для её оформления необходимо умение грамотно и наглядно выполнять чертежи и геометрические построения: чертить четырехугольники, находить середины их сторон, строить перпендикулярные прямые, откладывать на них равные отрезки. Существенную помощь в данной проблеме оказали возможности программы GeoGebra, переведенной на 39 языков и работающей на большом числе операционных систем. GeoGebra предоставляет пользователю набор виртуальных чертежных инструментов, с помощью которых на экране, как на листе бумаги, можно выполнять геометрические построения. Важнейшей особенностью полученного чертежа является то, что программа запоминает алгоритм построения, исходные данные можно легко изменять и результат сохранить в удобном формате.
Рассмотрим теорему Вариньона и пару следствий из неё.
Теорема Вариньона (рисунок 1): Четырехугольник, образованный путем последовательного соединения середин сторон выпуклого четырехугольника, является параллелограммом, и его площадь равна половине площади данного четырехугольника.
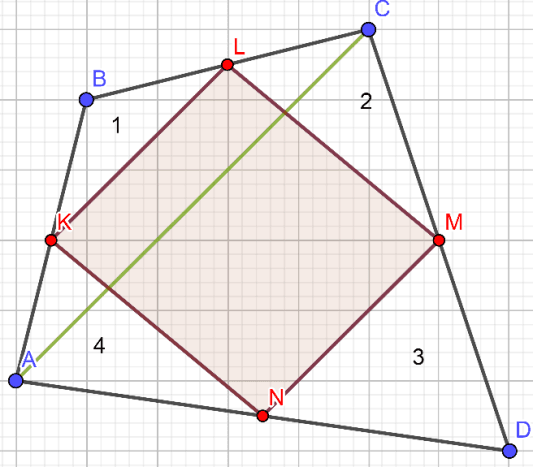
Рис. 1
Дано:
ABCD – выпуклый четырехугольник
AK=KB; BL=LC; CM=MD; AN=ND.
Доказать:
- KLMN – параллелограмм;
- SKLMN= SABCD:2
Доказательство:
- Рассмотрим одну из сторон четырехугольника KLMN, например NM. Так как NM является средней линией треугольника ADC, то NM ║AC. По тем же причинам KL║AC. Следовательно, KL║NM и KL= MN= AC:2. таким образом, по признаку KLMN – параллелограмм. Этот параллелограмм называется параллелограммом Вариньона данного четырехугольника
- Средняя линия треугольника отсекает от него треугольник, площадь которого в четыре раза меньше площади исходного треугольника. Поэтому сама сумма площадей первого и третьего треугольников равна четверти площади всего четырехугольника. То же и относительно суммы площадей второго и четвертого треугольников. Поэтому площадь параллелограмма KLMN составляет половину площади четырехугольника
Некоторые следствия из теоремы Вариньона:
Следствие 1.
Параллелограмм Вариньона является ромбом тогда и только тогда, когда в исходном четырехугольнике: а) диагонали равны; б) бимедианы перпендикулярны.
а) Прямая теорема (рисунок 2): если в четырёхугольнике диагонали равны, то параллелограмм Вариньона является ромбом.
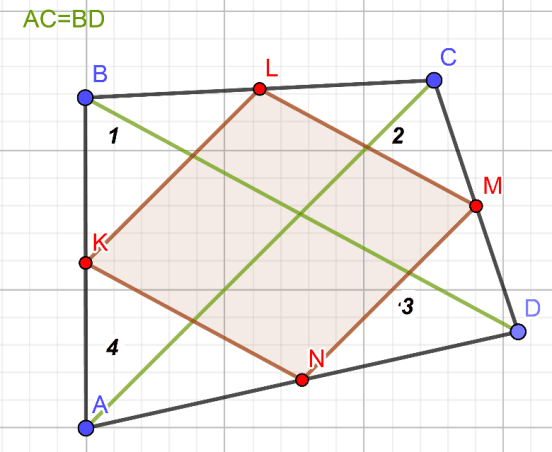
Рис. 2
Дано:
ABCD – четырехугольник;
KLMN – параллелограмм Вариньона;
AC=BD
Доказать: KLMN – ромб.
Доказательство:
Так как AC=BD (диагонали исходного четырехугольника равны по условию), то стороны параллелограмма Вариньона будут равны KL=LM=MN=NK (используя свойство средних линий треугольников, образованных при пересечении диагоналей исходного четырехугольника). Параллелограмм c равными сторонами является ромбом.
Обратная теорема: если параллелограмм Вариньона является ромбом, то диагонали исходного четырёхугольника равны.
б) Прямая теорема (рисунок 3): если в четырёхугольнике бимедианы перпендикулярны, то параллелограмм Вариньона является ромбом.
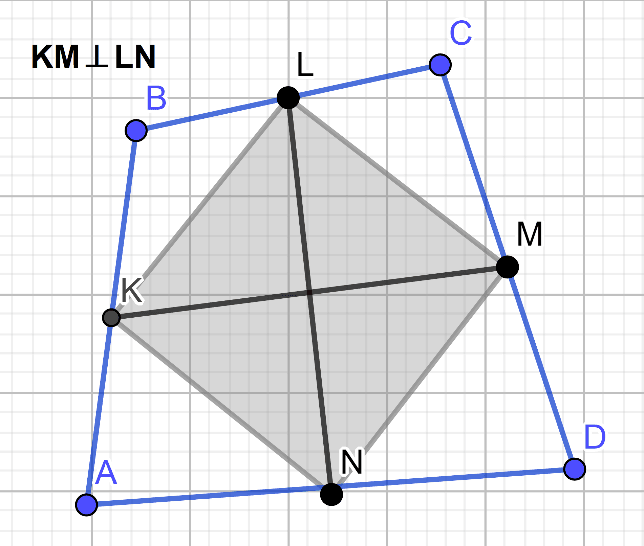
Рис. 3
Дано:
ABCD – четырехугольник;
KLMN – параллелограмм Вариньона;
KM и LN перпендикулярны
Доказать: KLMN – ромб.
Доказательство:
Бимедианы исходного четырехугольника – это диагонали параллелограмма Вариньона. Так как в параллелограмме диагонали перпендикулярны, то этот параллелограмм является ромбом (по признаку ромба).
Обратная теорема: если параллелограмм Вариньона является ромбом, то бимедианы исходного четырёхугольника перпендикулярны.
Следствие 2.
Параллелограмм Вариньона является прямоугольником тогда и только тогда, когда в исходном четырехугольнике: а) диагонали перпендикулярны; б) бимедианы равны.
а) Прямая теорема (рисунок 4): если в четырёхугольнике диагонали перпендикулярны, то параллелограмм Вариньона является прямоугольником.
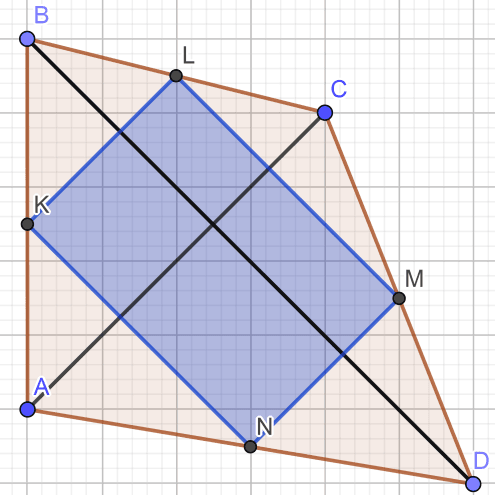
Рис. 4
Дано:
Четырехугольник ABCD;
KLMN – параллелограмм Вариньона;
диагонали AC и BD – перпендикулярны.
Доказать: KLMN – прямоугольник.
Доказательство:
Так как диагонали AC и BD – перпендикулярны, то стороны параллелограмма Вариньона будут перпендикулярны. Следовательно, параллелограмм Вариньона является прямоугольником.
Обратная теорема: если параллелограмм Вариньона является прямоугольником, то диагонали исходного четырёхугольника перпендикулярны.
б) Прямая теорема (рисунок 5): если в четырёхугольнике бимедианы равны, то параллелограмм Вариньона является прямоугольником.
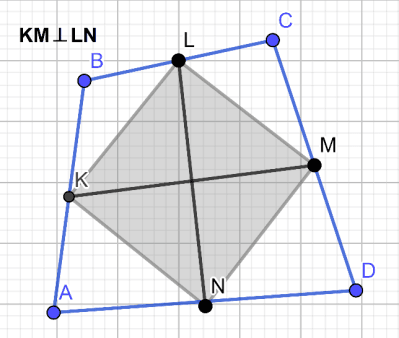
Рис. 5
Дано:
Четырехугольник ABCD;
KLMN – параллелограмм Вариньона;
бимедианы KM и LN – равны.
Доказать: KLMN – прямоугольник.
Доказательство:
Бимедианы исходного четырехугольника – это диагонали параллелограмма Вариньона. Так как в параллелограмме диагонали равны, то этот параллелограмм является прямоугольником (по признаку прямоугольника).
Обратная теорема: если параллелограмм Вариньона является прямоугольником, то бимедианы исходного четырёхугольника равны.
Сравнение решений задач с использованием теоремы Вариньона и без её применения:
Задача 1. Докажите, что середины сторон четырехугольника являются вершинами параллелограмма (рисунок 6).
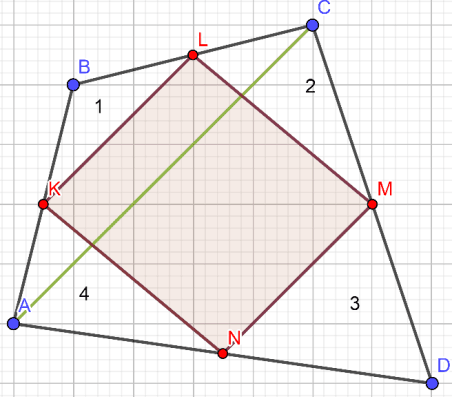
Рис. 6
Дано: ABCD – четырехугольник
AK=KB, BL=LC, CM=MD, AN=ND
Доказать: KLMN – параллелограмм.
Доказательство:
1 способ
Проведем АС и рассмотрим треугольник АВС. KL – средняя линия, следовательно KL║ AC, KL= AC:2. Рассмотрим треугольник ADC, NM – средняя линия, следовательно NM║AC, NM = AC/2.
KL║ AC, NM ║AC, следовательно, KL ║NM.
KL= AC:2, NM = AC:2, следовательно, KL=NM.
KLMN – параллелограмм (противоположные стороны равны и параллельны)
2 способ
KLMN – параллелограмм Вариньона (по определению).
Задача 2. Докажите, что площадь параллелограмма, вершины которого являются серединами сторон четырехугольника ABCD, равна половине площади четырехугольника ADCD (рисунок 7).
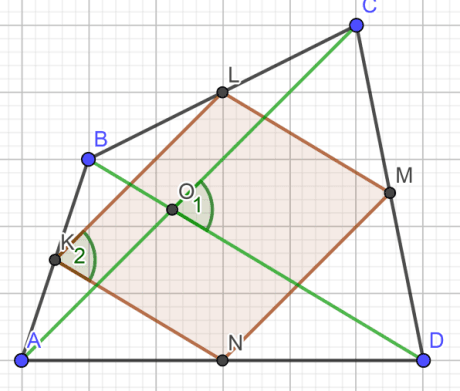
Рис. 7
Дано: ABCD – четырехугольник
Доказать: SKLMN=1/2 SABCD
Доказательство:
1 способ
Так как SABCD=1/2ACXBD sin<1 и SKLMN=1/2KLXKN sin<2 и учитывая, что <1=<2, KL=1/2AC и KN=1/2BD, то получаем, что SKLMN=1/2 SABCD
2 способ
Так как KLMN – параллелограмм Вариньона, то его площадь равна половине площади четырехугольника ABCD.
Задача 3. Докажите, что середины сторон прямоугольника являются вершинами ромба. И наоборот (рисунок 8).
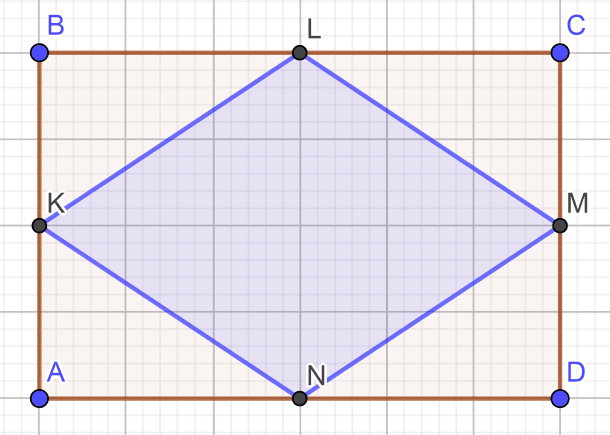
Рис. 8
Доказательство:
1 способ
- AC – диагональ. KL – средняя линия треугольника ABC. NM – средняя линия треугольника ADC. Треугольники ABC и ADC равны по третьему признаку равенства треугольников (AB=DC, BC=DC, AC – общая сторона) => KL=NM. Также KL||NM (AC||NM, AC||KL) => KLMN- параллелограмм.
- Из первого следует, что KL=NM. Аналогично можно доказать, что LM=KN.
- ABCD – прямоугольник => AC=BD. => KL=LM=MN=NK=> KLMN – ромб.
2 способ
а) Диагонали прямоугольника равны, поэтому середины сторон прямоугольника являются вершинами ромба;
б) Стороны прямоугольника перпендикулярны, поэтому бимедианы перпендикулярны, тогда середины сторон прямоугольника являются вершинами ромба.

.png&w=640&q=75)