Introduction
In today’s dynamic environment, companies must make appropriate decisions to keep the organization stable, achieve and maintain any competitive advantage. Most businesses recognize the value of intercompany relationships in maintaining a competitive structure and increasing market share. As a result, companies began to re-establish their relationships with providers and consumers based on partnership and the creation of shared values. The partnership formed with suppliers provides advantages for both quality improvement and cost-saving, while also boosting production flexibility.
Choosing a server is a decision-making problem that considers many criteria to obtain a result. As the complexity of the problem increases, it is getting harder to make the correct decision. To solve this kind of problem, scientific methods have become a requirement.
The goal of this study is to help a company choose the right server considering the given criteria. For this problem, the TOPSIS problem is recommended, as this problem is one of multi-criteria decision-making methods. The Fuzzy TOPSIS helps choose the right alternative based on the linguistic variables.
Definition of a problem
The selection of a server is a complex problem because we have to make a decision based on multiple criteria. There are two types of criteria. They are objective and subjective criteria.
Objective criteria are measurable. As objective criteria following are used in the server selection problem [2]:
- Price (AZN)
- RAM capacity (GB)
- Processor speed (GHz)
- Number of cores
- Hard disk capacity (TB)
Subjective criteria aren’t measurable like objective ones. They are defined based on expert reviews and experience. As subjective criteria following are used in the server selection problem:
- Reliability
- Security
- Scalability
- Quality of services
To solve this problem, we propose the fuzzy TOPSIS method is used. There are 7 stages of the TOPSIS method. They are:
1. Define linguistic variables for both criteria and the decision (table 1, table 2).
Table 1
Linguistic variables for criteria
|
Linguistic variables |
Triangular fuzzy numbers |
|
Very Low(VL) |
(1,1,3) |
|
Low(L) |
(1,3,5) |
|
Medium(M) |
(3,5,7) |
|
High(H) |
(5,7,9) |
|
Very High(VH) |
(7,9,9) |
Table 2
Linguistic variables for decision
|
Linguistic variables |
Triangular fuzzy numbers |
|
Very Low(VL) |
(0.1,0.1,0.1,0.3) |
|
Low(L) |
(0.1, 0.3, 0.5) |
|
Medium(M) |
(0.3, 0.5, 0.7) |
|
High(H) |
(0.5, 0.7, 0.9) |
|
Very High(VH) |
(0.7, 0.9, 0.9) |
2. The decision matrix has to be normalized using the following formula [3, 4]:
= 
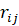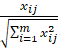
3. This step is called a “normalized matrix”. The weight is defined as wj=(w1, w2, …, wn). wj is the criteria for all j from 1 to n. The normalization of the matrix is denoted with the V. Vij = wj* rij
4. In the 3rd step, we have to determine the ideal solution matrix of both the positive ideal and negative ideal [5]. The formula is as follows:
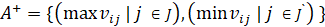, i = 1, 2, … m
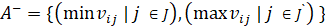, i = 1, 2, … m
5. In this step, the separation is calculated [6].
Ideal separation: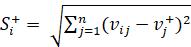 
Negative separation: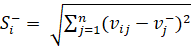 
6. The positive ideal solution is calculated with the following formula [7, 8]:
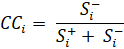
7. In the final step, we have to rank the solution. The solution with the highest value of CCi is the best solution.
8. Acceptance criteria (table 3).
Table 3
Acceptance criteria
|
Closeness Coefficient (CCi) |
Evaluation |
|
|
Not recommended |
|
|
Recommended with high risk |
|
|
Recommended with low risk |
|
|
Acceptable |
|
|
Accepted and preferred |
Practical example. In this example, we are going to consider server selection problem 9 criteria and 5 alternatives.
C1-Price (AZN)
C2- RAM capacity (GB)
C3-Processor speed (GHz)
C4-Number of cores
C5-Hard disk capacity (TB)
C6-Reliability
C7-Security
C8-Scalability
C9-Quality of services
1. Representation of linguistic decision matrix (table 4).
Table 4
Linguistic decision matrix
|
|
A1 |
A2 |
A3 |
A4 |
A5 |
|
C1 |
L |
M |
H |
L |
VH |
|
C2 |
M |
H |
VH |
VL |
H |
|
C3 |
H |
M |
M |
H |
VH |
|
C4 |
M |
VH |
H |
M |
VH |
|
C5 |
L |
M |
VH |
M |
VH |
|
C6 |
VL |
H |
M |
L |
VH |
|
C7 |
M |
VL |
H |
M |
H |
|
C8 |
H |
M |
L |
M |
L |
|
C9 |
M |
H |
VH |
H |
M |
The weight importance vector is: w=(H,VH,M,L,H,M,VH,L,H)
2. Convert linguistic variables into triangular fuzzy numbers (table 5).
Table 5
Triangular fuzzy numbers presentation
|
|
A1 |
A2 |
A3 |
A4 |
A5 |
|
C1 |
(1,1,3) |
(3,5,7) |
(5,7,9) |
(1,3,5) |
(7,9,9) |
|
C2 |
(3,5,7) |
(5,7,9) |
(7,9,9) |
(1,1,3) |
(5,7,9) |
|
C3 |
(5,7,9) |
(3,5,7) |
(3,5,7) |
(5,7,9) |
(7,9,9) |
|
C4 |
(3,5,7) |
(7,9,9) |
(5,7,9) |
(3,5,7) |
(7,9,9) |
|
C5 |
(1,3,5) |
(3,5,7) |
(7,9,9) |
(3,5,7) |
(7,9,9) |
|
C6 |
(1,1,3) |
(5,7,9) |
(3,5,7) |
(1,3,5) |
(7,9,9) |
|
C7 |
(3,5,7) |
(1,1,3) |
(5,7,9) |
(3,5,7) |
(5,7,9) |
|
C8 |
(5,7,9) |
(3,5,7) |
(1,3,5) |
(3,5,7) |
(1,3,5) |
|
C9 |
(3,5,7) |
(5,7,9) |
(7,9,9) |
(5,7,9) |
(3,5,7) |
3. Normalized fuzzy decision-matrix is calculated by the given formula (table 6).
Table 6
Normalized fuzzy decision-matrix
|
|
A1 |
A2 |
A3 |
A4 |
A5 |
|
C1 |
(0.33,1,1) |
(0.14,0.2,0.33) |
(0.11,0.14,0.2) |
(0.2,0.33,1) |
(0.11,0.11,0.14) |
|
C2 |
(0.33,0.56,0.78) |
(0.56,0.78,1) |
(0.78,1,1) |
(0.11,0.11,0.33) |
(0.56,0.78,1) |
|
C3 |
(0.56,0.78,1) |
(0.33,0.56,0.78) |
(0.33,0.56,0.78) |
(0.56,0.78,1) |
(0.78,1,1) |
|
C4 |
(0.33,0.56,0.78) |
(0.78,1,1) |
(0.56,0.78,1) |
(0.33,0.56,0.78) |
(0.78,1,1) |
|
C5 |
(0.11,0.33,0.56) |
(0.33,0.56,0.78) |
(0.78,1,1) |
(0.33,0.56,0.78) |
(0.78,1,1) |
|
C6 |
(0.11,0.11,0.33) |
(0.56,0.78,1) |
(0.33,0.56,0.78) |
(0.11,0.33,0.56) |
(0.78,1,1) |
|
C7 |
(0.33,0.56,0.78) |
(0.11,0.11,0.33) |
(0.56,0.78,1) |
(0.33,0.56,0.78) |
(0.56,0.78,1) |
|
C8 |
(0.56,0.78,1) |
(0.33,0.56,0.78) |
(0.11,0.33,0.56) |
(0.33,0.56,0.78) |
(0.11,0.33,0.56) |
|
C9 |
(0.33,0.56,0.78) |
(0.56,0.78,1) |
(0.78,1,1) |
(0.56,0.78,1) |
(0.33,0.56,0.78) |
4. The weighted normalized decision matrix is calculated (table 7).
Table 7
Weighted normalized decision matrix
|
|
A1 |
A2 |
A3 |
A4 |
A5 |
|
C1 |
(0.17,0.7,0.9) |
(0.07,0.14,0.3) |
(0.06,0.1,0.18) |
(0.1,0.23,0.9) |
(0.06,0.08,0.13) |
|
C2 |
(0.23,0.5,0.7) |
(0.39,0.7,0.9) |
(0.54,0.9,0.9) |
(0.08,0.1,0.3) |
(0.39,0.7,0.9) |
|
C3 |
(0.17,0.39,0.7) |
(0.1,0.28,0.54) |
(0.1,0.28,0.54) |
(0.17,0.39,0.7) |
(0.23,0.5,0.7) |
|
C4 |
(0.03,0.17,0.39) |
(0.08,0.3,0.5) |
(0.06,0.23,0.5) |
(0.03,0.17,0.39) |
(0.08,0.3,0.5) |
|
C5 |
(0.06,0.23,0.5) |
(0.17,0.39,0.7) |
(0.39,0.7,0.9) |
(0.17,0.39,0.7) |
(0.39,0.7,0.9) |
|
C6 |
(0.03,0.06,0.23) |
(0.17,0.39,0.7) |
(0.1,0.28,0.54) |
(0.03,0.17,0.39) |
(0.23,0.5,0.7) |
|
C7 |
(0.23,0.5,0.7) |
(0.08,0.1,0.3) |
(0.39,0.7,0.9) |
(0.23,0.5,0.7) |
(0.39,0.7,0.9) |
|
C8 |
(0.06,0.23,0.5) |
(0.03,0.17,0.39) |
(0.01,0.1,0.28) |
(0.03,0.17,0.39) |
(0.01,0.1,0.28) |
|
C9 |
(0.17,0.39,0.7) |
(0.28,0.54,0.9) |
(0.39,0.7,0.9) |
(0.28,0.54,0.9) |
(0.17,0.39,0.7) |
5. The distance between the decisions is calculated (table 8).
Table 8
Distance between the decisions
|
|
C1 |
C2 |
C3 |
C4 |
C5 |
|
d(A1,A+) |
0.44 |
0.46 |
0.36 |
0.34 |
0.66 |
|
d(A2,A+) |
0.74 |
0.32 |
0.43 |
0.27 |
0.53 |
|
d(A3,A+) |
0.79 |
0.21 |
0.43 |
0.30 |
0.32 |
|
d(A4,A+) |
0.60 |
0.75 |
0.36 |
0.34 |
0.53 |
|
d(A5,A+) |
0.81 |
0.32 |
0.29 |
0.27 |
0.32 |
|
d(A1,A-) |
0.62 |
0.44 |
0.39 |
0.22 |
0.28 |
|
d(A2,A-) |
0.15 |
0.62 |
0.28 |
0.31 |
0.42 |
|
d(A3,A-) |
0.08 |
0.72 |
0.28 |
0.29 |
0.64 |
|
d(A4,A-) |
0.50 |
0.13 |
0.39 |
0.22 |
0.42 |
|
d(A5,A-) |
0.04 |
0.62 |
0.42 |
0.31 |
0.64 |
|
|
C6 |
C7 |
C8 |
C9 |
|
d(A1,A+) |
0.60 |
0.46 |
0.30 |
0.53 |
|
d(A2,A+) |
0.36 |
0.75 |
0.34 |
0.41 |
|
d(A3,A+) |
0.43 |
0.32 |
0.39 |
0.32 |
|
d(A4,A+) |
0.52 |
0.46 |
0.34 |
0.41 |
|
d(A5,A+) |
0.29 |
0.32 |
0.39 |
0.53 |
|
d(A1,A-) |
0.12 |
0.44 |
0.31 |
0.33 |
|
d(A2,A-) |
0.44 |
0.13 |
0.24 |
0.48 |
|
d(A3,A-) |
0.33 |
0.62 |
0.16 |
0.54 |
|
d(A4,A-) |
0.22 |
0.44 |
0.24 |
0.48 |
|
d(A5,A-) |
0.48 |
0.62 |
0.16 |
0.33 |
As the final step, the closeness coefficient is calculated by the given formula (table 9.)
Table 9
Closeness coefficients
|
|
|
|
CCi |
Ranking |
|
A1 |
4.15 |
3.15 |
0.431 |
3 |
|
A2 |
4.14 |
3.07 |
0.426 |
4 |
|
A3 |
3.50 |
3.66 |
0.512 |
2 |
|
A4 |
4.31 |
3.04 |
0.413 |
5 |
|
A5 |
3.54 |
3.64 |
0.508 |
1 |
According to the acceptance criteria A5 is the optimal decision.
Conclusion
The topic of MCDM for server selection is the focus of this essay. In today’s environment, companies need to choose the right server among many decisions. The right server is a server that has the lowest price and the best quality. The selection process is complex because there are uncertainties as the decision-makers are individuals. An examination of known strategies for resolving this challenge is provided. The fuzzy TOPSIS approach is utilized to solve this problem. The challenges of the actual application of this approach are thoroughly examined. The server selection problem with 9 criteria and 5 choices is viewed as a practical challenge. The criteria were price, ram capacity, processor speed, number of cores, hard disk capacity, reliability, security, scalability, and quality of service. After the closeness coefficient is calculated, it shows that A5 is the best alternative among other given alternatives. For that reason, it is recommended for small businesses to choose that alternative. The solution’s findings at each stage are provided.
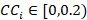
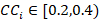
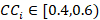
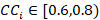
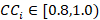
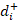
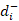
.png&w=640&q=75)
