Волны Гёртлера на внутренней поверхности сопла АДТ с профилем Витошинского

1. Поток на входе в сопло на вогнутой части поверхности сопла может создавать в пограничном слое на поверхности сопла волны Гёрлера, состоящие из продольно направленных вихрей. Для их образования необходимо, чтобы критерий Гёртлера G 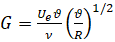[1]

,     (1)

здесь U_e – скорость на внешней границе пограничного слоя, ϑ – толщина потери импульса, ν – вязкость, R – радиус продольной кривизны внутренней поверхности сопла, превышал некоторую величину [1]. При дальнейшем увеличении G пограничный слой становится турбулентным. Кроме того, звуковые возмущения, возникающие на срезе сопла дозвуковой АДТ, могут проникать вверх по потоку [2, 3], и возбуждать пограничный слой. Эти возмущения, возможно усиленные вниз по потоку, будут возбуждать колебания слоя смешения на выходе из сопла и, тем самым, усиливать шум вытекающей струи. Для оценки этого сценария развития возмущений представляет интерес возбуждение волн Гёртлера [4, 5, 6] на вогнутой части АДТ, для чего необходимо определить характеристики пограничного слоя, образующегося на ее внутренней поверхности. При этом будем считать, что в сопло втекает равномерный по радиусу поток.

Далее для определения характеристик пограничного слоя на внутренней, вогнутой, поверхности сопла АДТ использованы уравнения Прандтля для сжимаемого газа в переменных Мизеса (см. [7]). Форма сопла определяется профилем Витошинского (рис. 1).

.

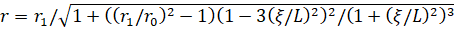Здесь r₁ – радиус начального сечения сопла, r₀ – радиус конечного сечения сопла, r – радиус поперечного сечения сопла в точке ξ (проекция точки контура на ось сопла), M₁ – число Маха в начальном сечении, 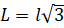, l – длина криволинейного участка сопла по контуру). Далее принято l=1, r₁=0.925, r₀=0.35.

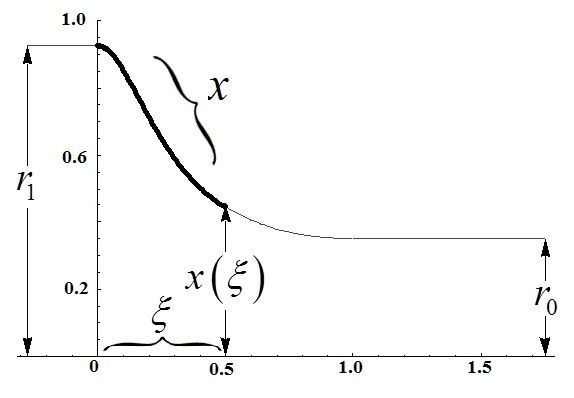
Рис. 1. Контур сопла АДТ, ξ – координата вдоль оси сопла, x(ξ) – координата вдоль искривленной части сопла

Для упрощения расчетов параметры невязкого течения определены по одномерной теории [8]: зависимость числа Маха от величины площади сечения трубы с круглым сечением

,

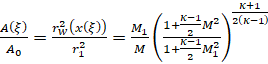Здесь A(ξ), M – соответственно сечение сопла в текущем положении ξ продольной координаты, число Маха, A₀, M₁ – соответственно начальное сечение и число Маха в этом сечении, 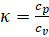 – отношение теплоемкостей.

Зависимость аэродинамических величин от числа Маха:

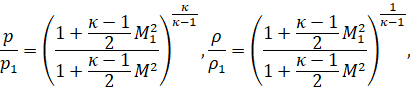
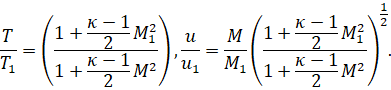
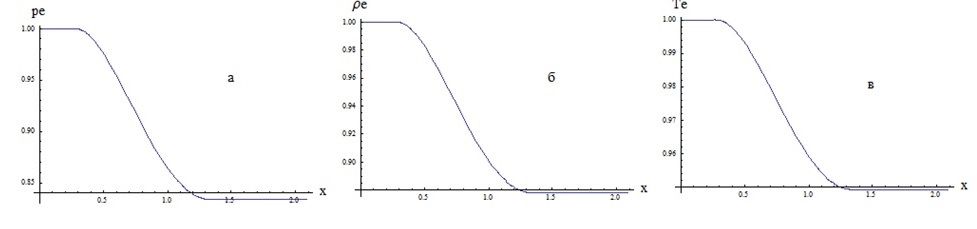
Рис. 2. а, б, в. Распределение p_e, ρ_e, T_e на внешней границе пограничного слоя в зависимости от координаты вдоль контура сопла

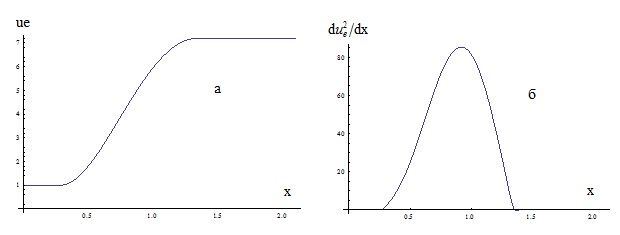
Рис. 3 а, б. Распределение 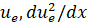 на внешней границе пограничного слоя в зависимости от координаты вдоль контура сопла

На рисунках 2 а, б, в и 3 а, б представлены зависимости аэродинамических величин внутри сопла от длины дуги профиля сопла.

2. Уравнения пограничного слоя для ламинарных установившихся течений сжимаемого совершенного газа имеет следующий вид [1]:

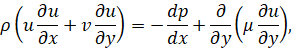
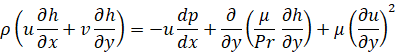
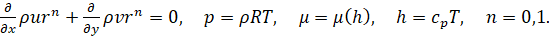 (2)

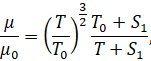
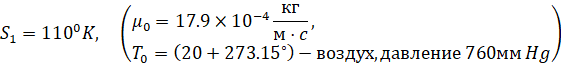
Здесь и далее принято: x, y – расстояния, отсчитываемые вдоль поверхности сопла от его начала и по нормали от поверхности соответственно; u,v – составляющие скорости в направлениях x и y соответственно, ρ – плотность, p – давление, h – энтальпия, T – температура, R – газовая постоянная, μ – коэффициент вязкости, r – радиус поперечного сечения сопла, Pr – число Прандтля, n – безразмерный параметр n = 0 – плоский случай, n = 1 – осесимметричный случай. Во внешнем течении имеем

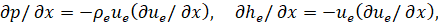
граничные условия:

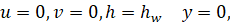
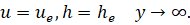
Переменные Мизеса x, ψ (см., например, [7]): ψ – функция тока 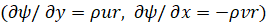, x – длина дуги сопла от его начала,  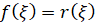– форма образующей поверхности сопла, ξ – координата вдоль оси сопла. Зависимость длины дуги (x) от координаты вдоль оси ξ определяется соотношением:

, .

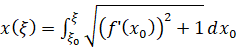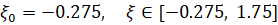На рисунках 4 а, б эта зависимость представлена в графическом виде. Отрицательные значения переменной ξ соответствуют части сопла постоянного радиуса (см. рис. 1).

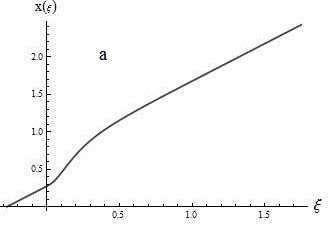
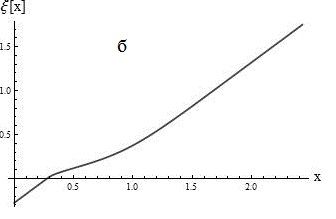
Рис. 4 а, б. Зависимость длины контура сопла от продольной координаты (а) и обратная зависимость координаты вдоль оси сопла от длины дуги вдоль контура сопла (б)

Уравнения пограничного слоя (2) в новых переменных примут вид

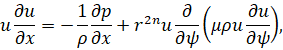
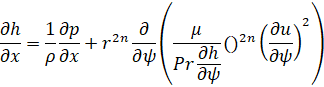
u=0, h=h_w ψ=0;

u=u_e, h=h_e ψ→∞.    (3)

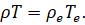
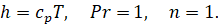
rξ - здесь радиус сопла в данной точке на оси. Величина 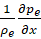 представлена как .

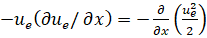Отнесем все величины к их значениям в точке 1 (начало сопла) 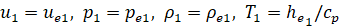. Кроме того, введем безразмерные величины

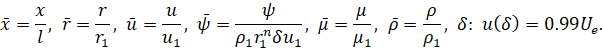
Здесь δ – характерная толщина пограничного слоя в физическом пространстве. Тогда перед вязким членом возникает множитель 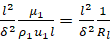. Полагая этот множитель равным 1 получим 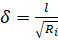. Безразмерная толщина потери импульса в сжимаемом газе определяется выражением [1]

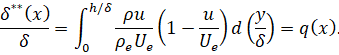
В данном случае x – расстояние вдоль дуги контура сопла. В этом выражении предполагается, что толщина пограничного слоя много меньше радиуса сопла.

В безразмерных переменных для уравнений (3) получим

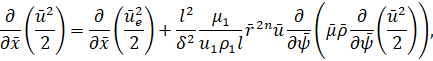
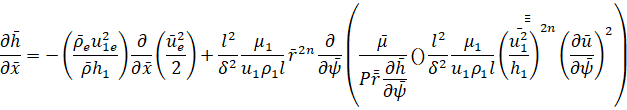
u=0, h=h_w ψ=0;

u=u_e, h=h_e, ψ→∞,

.

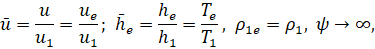
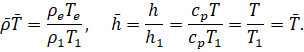
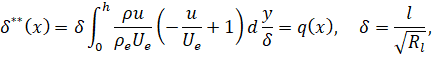
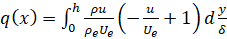3. Для определения возможности возникновения вихрей Гёртлера выпишем еще выражение для радиуса кривизны дуги: .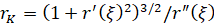

На рис. 5 представлена зависимость кривизны профиля Витошинского от координаты вдоль оси сопла.

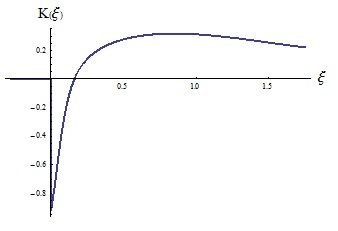
Рис. 5. Кривизна контура сопла как функция продольной координаты

Для получения численного решения в качестве исходных числовых величин примем следующие значения

 

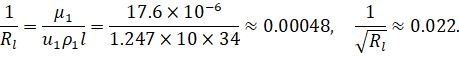
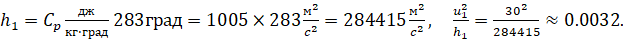
Для вязкости воспользуемся формулой Сазерленда:

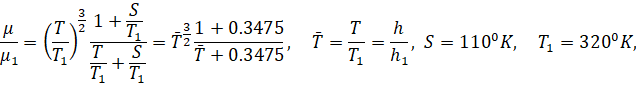
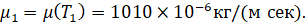
Уравнения (3) решены с помощью пакета прикладных программ [12]. Распределение скорости и энтальпии представлено на рис. 6 а, б в пограничном слое на внутренней поверхности АДТ.

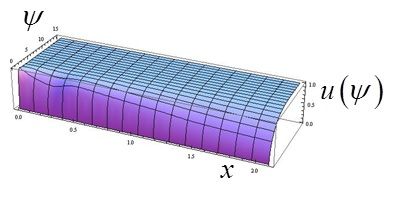
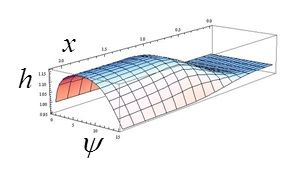
Рис. 6, а) распределение продольной скорости в зависимости от длины дуги профиля сопла; б) распределение энтальпии в зависимости от длины дуги профиля сопла

На рис.6 а, б. представлено распределение скорости и энтальпии в ламинарном пограничном слое на внутренней поверхности сопла.

Возникновение вихрей Гёртлера связано с числом Гёртлера G (см. [1, 4, 5]), которое в данном случае можно представить следующим образом:

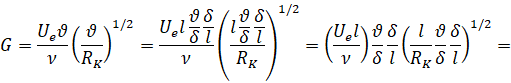
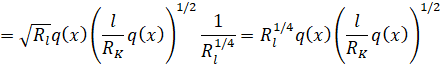
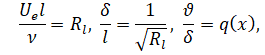
R_K – радиус кривизны вогнутой части сопла. Здесь U_e – скорость на внешней границе пограничного слоя, ϑ – толщина потери импульса, ν – кинематическая вязкость, R_K – радиус кривизны поверхности. Вихри Гертлера возникают, если число Гертлера G > 0.3. При G > 7 происходит турбулизация пограничного слоя. На рис. 7 а, б приведено поведение толщины потери импульса в пограничном слое и критерия G на внутренней поверхности сопла в зависимости от координаты ξ на оси.

Величина толщины потери импульса ϑ определяется выражением

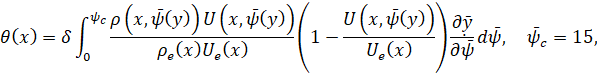
Якобиан пересчета на физические координаты можно записать как

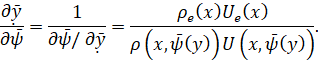
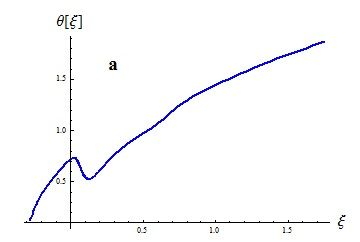
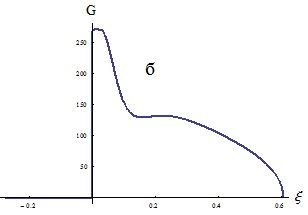
Рис. 7, а) толщина потери импульса в зависимости от координаты вдоль оси; б) Величина критерия Гёртлера в зависимости от координаты вдоль оси

На рис. 7 а,б представлены толщина потери импульса θ(ξ) (рис. 7,а) и критерий Гёртлера G(ξ) (рис. 7,б) возникновения продольных вихрей. Здесь ξ – координата вдоль продольной оси. Равенство нулю критерия Гёртлера при отрицательных значениях ξ обусловлено равенством нулю кривизны на горизонтальном участке сопла.

Величина G превосходит граничное значение 0.3 [1], 0.58 [3], т.е. волны Гёртлера возбуждаются. Более того, G превосходит критическое значение G_cr = 7 [1], при котором происходит турбулизация пограничного слоя. Таким образом, критерий G указывает на образование продольных вихрей Гёртлера в начальной части сопла и интенсивную турбулизацию пограничного слоя. Практика показывает, что образовавшиеся возмущения потока в пограничном слое не исчезают и не ослабевают вниз по потоку, даже если критерий G возбуждения волн Гёртлера уже перестает выполняться. Так что можно ожидать сильного влияния волн Гёртлера на слой смешения, который образуется при выходе струи газа из сопла. В работах [9, 10, 11] рассмотрена возможность воздействия на волны Гёртлера. При этом указывается возможность их эффективного подавления. Таким образом, возможность влияния на вихри Гёртлера в принципе имеется и, тем самым, имеется возможность влияния на генерацию шума на выходе из сопла.

Все вычисления произведены с помощью пакета MARHEMATICA [12].