Об устойчивом взаимном отслеживании движений реального динамического объекта и его виртуальной модели-поводыря

Введение. В работе для векторной линейной конфликтно-управляемой динамической системы решается задача обеспечивающим близость (взаимное отслеживание) движений реального объекта и его виртуальной модели-лидера или модели-поводыря в схеме управления по принципу обратной связи. Такая задача часто возникает в задачах оптимального управления при дефиците информации о действующих на систему динамических помехах. Такие задачи входят в круг задач, рассматривающихся в теории антагониститческих дифференциальных игр [1-8]. В работе задача решается методом экстремального сдвига, разработанного авторами [3, 7, 8].

Управляемый объект. Рассматривается объект, движение которого описывается обыкновенным векторным дифференциальным уравнением

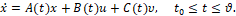
Здесь x – n-мерный фазовый вектор управляемого объекта; t – время, моменты времени начальный t₀ и конечный ϑ зафиксированы; u – r-мерный вектор управления, υ – s-мерный вектор помехи. Точка над буквой обозначает производную по времени. Все векторы трактуются как векторы-столбцы, т.е. в матричной форме уравнение (1) принимает вид

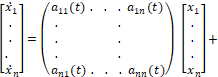
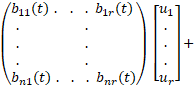      (2)

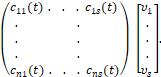
где компоненты всех матриц являются кусочно-непрерывными функциями, и векторы управления и помехи стеснены условиями

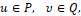 (3)

P и Q – ограниченные замкнутые множества – компакты.

Модель-поводырь. Следуя концепции антагонистических дифференциальных игр, разрабатываемой в Свердловске (ныне Екатеринбурге) в школе академика Красовского, при решении таких игр в схему управления по принципу обратной связи обычно вводится некоторая виртуальная модель-поводырь [4, 5, 7, 8]. Содержательно это лидер, за которым следует движение реального объекта для решения задачи при том или ином критерии качества процесса управления [4, 8]. Основной особенностью модели-поводыря является то, что в ней мы (первый игрок) можем распоряжаться всеми параметрами без каких-либо помех.

Итак, наряду с реальным динамическим объектом (1)-(3) рассмотрим некоторую его виртуальную (компьютерную) модель, имеющую такую же структуру при замене символов u на u_* и υ на υ_*, т.е.:

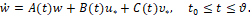 (4)

Здесь w – n-мерный фазовый вектор управляемого объекта; t – время, моменты времени начальный t₀ и конечный ϑ такие же, как в (1); u*– r-мерный вектор первого управления моделью, υ_*– s-мерный вектор первого управления моделью, и векторы управлений стеснены условиями

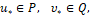(5)

где P и Q – компакты из (3).

Взаимное отслеживание движений объекта и модели. Построим n-мерный вектор

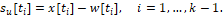
выбором управлений

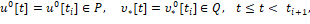
исходя из условий экстремального сдвига [3, 7, 8]:

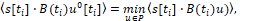(6) 

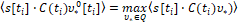
приходим к следующему утверждению.

Теорема. Если для объекта, описываемого дифференциальным уравнением (1)-(3), и его виртуальной модели-поводыря (4), (5) управления 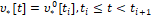 из условий экстремальных сдвигов (6), то при любых помехе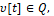 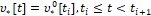  для объекта и управлении  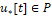для модели реализуются такие движения  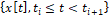и управления 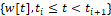, для которых будут выполнятся условия близости (взаимного отслеживания движений объекта и модели)

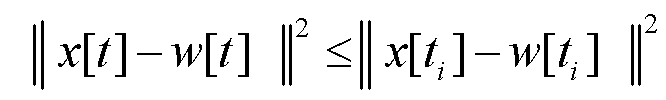
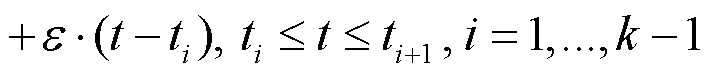
для любого сколь угодно малого ε>0.

При доказательстве этого утверждения используются соответствующие конструкции из работы авторов [7].