Задание различной пространственной ориентации элементов составного хаотического мультиаттрактора

Фазовое пространство динамической системы имеющей составной хаотический мультиаттрактор, можно представить как совокупность ячеек, каждая из которых содержит локальный хаотический аттрактор, которому соответствует локальная система координат, отвечающая исходным уравнениям движения [1-5].

Для того чтобы иметь возможность задавать различную пространственную ориентацию локальных аттракторов, необходимо ввести в уравнения движения дополнительные константы, задающие поворот локальных систем координат относительно исходного координатного базиса, и присвоить им различные значения в каждой фазовой ячейке.

Пусть исходная автостохастическая система задана в системе координат :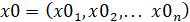

,    (1)

где  – множество констант.

Запишем её в новой системе координат , имеющей общий центр с системой координат x0, но повернутой на некоторый угол Ψ относительно проходящей через начало координат оси с направляющими косинусами 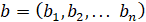 [6]:

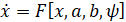.    (2)

Мультиаттракторная система на основе уравнений (2) в общем виде будет выглядеть следующим образом [3, 5]:

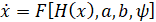,    (3)

где 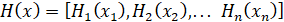 – множество реплицирующих операторов.

Чтобы каждый локальный аттрактор получил индивидуальную пространственную ориентацию, заменим в уравнениях (3) константы y и b специальными нелинейными функциями (назовем их ориентирующими), присваивающими этим константам различные значения в пределах каждой ячейки фазового пространства:

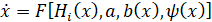,    (4)

где b(x) и Ψ(x) – ориентирующие функции, задающие соответственно оси поворота и величины углов поворота локальных систем координат в каждой фазовой ячейке.

Так как при повороте локального аттрактора изменяются его протяженность по переменным репликации и положение относительно границ содержащей его фазовой ячейки, в уравнения (4) необходимо ввести также масштабирующие и симметрирующие функции, задающие индивидуальные значения масштабирующих и симметрирующих коэффициентов в каждой фазовой ячейке [5]. В окончательном виде уравнения динамической системы, имеющей мультиаттрактор, состоящий из различно ориентированных хаотических аттракторов системы (1) будут иметь вид:

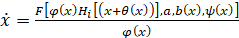,    (5)

где Θ(x) и Φ(x) – соответственно симметрирующие и масштабирующие функции.

Проиллюстрируем результат применения данной технологии на следующем примере. В качестве исходной динамической системы используем вариант уравнений Лоренца:

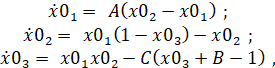    (6)

отличающийся от классической формы записи [7] тем, что стационарные особые точки лежат на координатной оси ОХ₁ (рис.1).

Рис. 1. Проекция аттрактора системы (6) на плоскость (x₁, x₃) при А=10.5, В=28, С=8/3

Рассмотрим вращение локальных аттракторов в мультиаттракторной системе, полученной из (6) заменой независимых переменных x₁, x₃ реплицирующими операторами H₁(x₁), H₃(x₃), заданными уравнениями

    (13)

,     ,

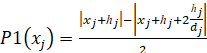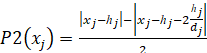где h_j – половина протяженности фазовой ячейки, содержащей хаотический аттрактор исходной динамической системы, по j-й переменной репликации, d_j – модуль крутизны промежуточных сегментов реплицирующей функции по j-й переменной репликации.

При вращении локальных аттракторов относительно осей ортогональных плоскости (x₁, x₃) уравнения (6) примут следующий вид:

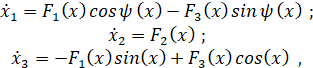    (7)

где

,

,

,

,

,

,

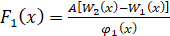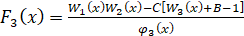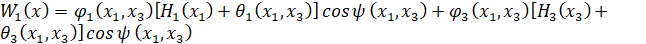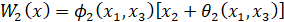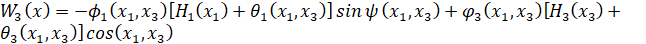где нелинейные функции y(x₁, x₃), f(x₁, x₃), q(x₁, x₃) задающие соответственно углы поворота локальных аттракторов, согласование их размеров и взаимное расположение в составе мультиаттрактора, определены следующими уравнениями:

,

, , ,

, , ,

,

, , ,

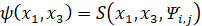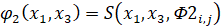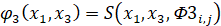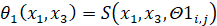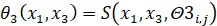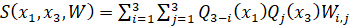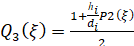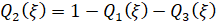где S(x₁,x₃,W) – структурная функция [5].

Пример композиционного мультиаттрактора с различной пространственной ориентацией локальных аттракторов, который может быть реализован в системе (7), приведен на рис.2. Ему соответствуют следующие значения констант Ψ, Φ, Θ:

, , ,

, , , .

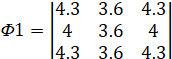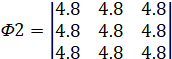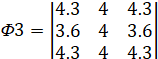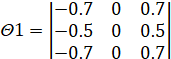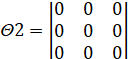Протяженность локальных аттракторов по всем независимым переменным выбрана равной 5, присвоением соответствующих значений коэффициентам Φ.

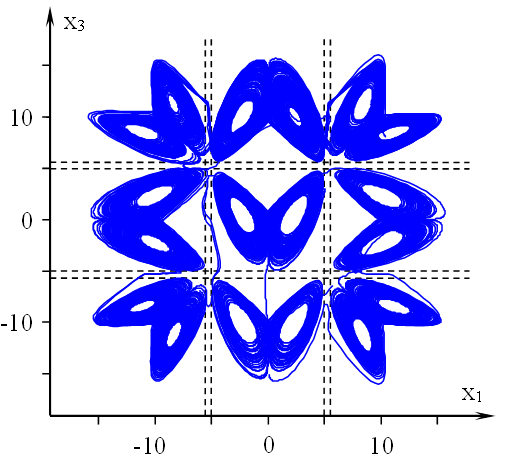
Рис. 2. Пример мультиаттрактора с заданной конфигурацией пространственной ориентации локальных аттракторов. Штриховыми линиями показаны границы фазовых ячеек