В школьном курсе геометрии не только изучаются различные геометрические модели (теоремы), но и рассматривается процесс их построения с использованием линейки и циркуля. Для создания геометрических моделей на компьютере удобно использовать системы компьютерного черчения.
Рассмотрим систему компьютерного черчения КОМПАС 3D, которая специально предназначена для обучения компьютерному черчению в школах. КОМПАС можно использовать для выполнения геометрических построений с помощью циркуля и линейки, а также при создании чертежей деталей.
КОМПАС 3D – компьютерное средство моделирования, являющееся комплексной системой автоматизированного проектирования. Компас 3D используется в приоритете для разработки чертежей, проектирования кабельных систем и создания документов для инженерных проектов [1, c. 153]. Однако программа имеет и свои недостатки: могут возникать проблемы при загрузке 3d моделей из других программ, проектирование в 3d сложнее для новичка, чем 2d, требуется полноценное освоение моделирования, не очень хорошая возможность визуализации объектов, система поверхностного моделирования имеет недостатки в оформлении.
Примером выполнения геометрических построений в программе используем задачу из практической работы 2.3 «Выполнение геометрических построений в системе компьютерного черчения КОМПАС» (по учебнику информатики за 9 класс Н.Д. Угриновича) [3, с. 128].
1. Постановки задачи
Задача: построить угол, равный данному углу.
Геометрические объекты, заданные в условии задачи: произвольный угол и отрезок.
2. Математическая модель
Математическая модель процесса геометрического построения зафиксирована в форме алгоритма:
1. С помощью Компактной панели вызвать панель Геометрия.
Выбрать объект Отрезок и построить сначала произвольный угол А (начертить два отрезка, выходящих из одной точки), а затем построить произвольный луч ОМ (начертить отрезок).
Введем обозначения точек на чертеже с помощью панели Обозначения.
2. С помощью Компактной панели вызвать панель Обозначения.
Щелкнуть по кнопке Ввод текста и последовательно ввести обозначения угла и концов отрезка.
Построим окружность произвольного радиуса с центром в вершине заданного угла А, которая пересечет стороны угла в точках В и С.
3. На панели Геометрия выбрать объект Окружность и построить окружность с центром в точке А.
На панели Обозначения щелкнуть по кнопке Ввод текста и обозначить точки пересечения окружности со сторонами угла буквами В и С.
Построим окружность того же радиуса с центром в начале заданного луча ОМ, которая пересечет отрезок в точке D.
4. На панели Геометрия выбрать объект Окружность.
На Панели свойств щелкнуть правой кнопкой мыши по полю Радиус и в контекстном меню выбрать пункт Между 2 точками.
На чертеже навести курсор сначала на точку А, а затем на точку В.
Центр появившейся окружности заданного радиуса переместить в точку О.
5. С помощью Компактной панели вызвать панель Обозначения. Щелкнуть по кнопке Ввод текста и обозначить точку пересечения окружности с отрезком ОМ буквой D.
Построим окружность с центром в точке D заданного радиуса ВС.
6. На панели Геометрия выбрать объект Окружность.
На Панели свойств щелкнуть правой кнопкой мыши по полю Радиус и в контекстном меню выбрать пункт Между 2 точками. На чертеже навести курсор сначала на точку С, а затем - на точку В.
Центр появившейся окружности заданного радиуса переместить в точку D.
7. С помощью Компактной панели вызвать панель Обозначения. Щелкнуть по кнопке Ввод текста и обозначить точку пересечения окружностей буквой Е.
8. Соединить отрезком точки О и Е, угол EOD, равный углу А, построен.
3. Компьютерная модель
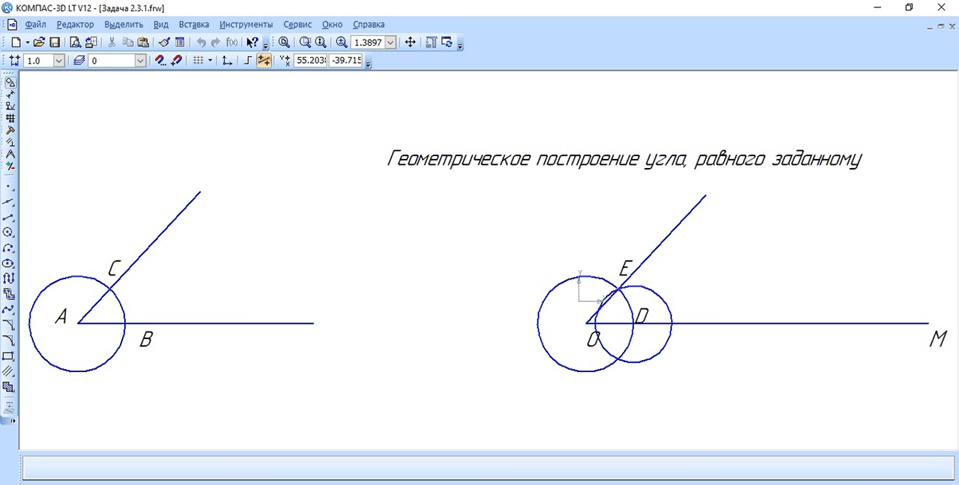
Рис. 1. Компьютерная модель построенного угла
4. Эксплуатация модели. Анализ полученных результатов
Анализ полученных результатов заключается в сравнении градусной меры данного и получившегося углов. Проведение анализа возможно при помощи панели Измерения. Анализ градусных мер углов показал, что оба угла (данный и полученный) равны по 47˚ (рис. 2).
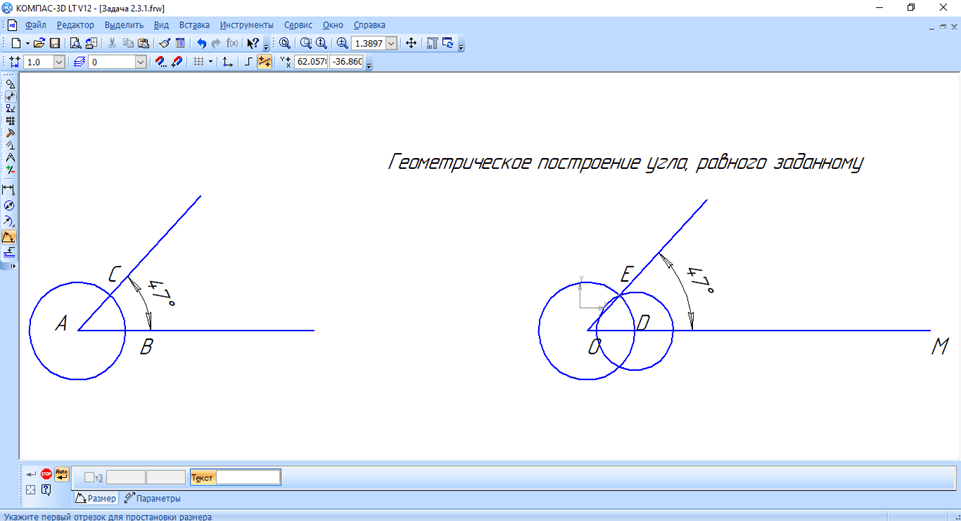
Рис. 2. Анализ полученных результатов
Таким образом, можно отметить, что в современных условиях учитель вправе реализовывать моделирование объектов в различных программных обеспечениях, средствах и пакетах, даже в ознакомительных целях [2, c. 16]. Это позволит современным школьникам не только научиться программировать в рамках раздела моделирование, но и самостоятельно ставить задачу, находить математические модели и области использования результатов решения задачи.

.png&w=640&q=75)