Задача конфликтного управления при запаздывающей неточной информации о текущих состояниях объекта

Введение. Рассматривается в игровой постановке становке задача [1-10] оптимального управления по принципу обратной связи динамической системой, которая описывается векторным линейным дифференциальным уравнением. Особенность рассматриваемой задач – в неполноте информации о помехах, действующих на управляемый объект, а также запаздывании и неточной или искаженной информации о текущих состояниях управляемого объекта. Критерии качества процесса управления задаются в виде функционалов от движения объекта, управляющих воздействий и помех. Такие задачи занимают достаточно большое место среди задач управления в технике, экономике и т.д. Задача на минимакс выбранного критерия качества решается в рамках концепции, разрабатываемой в уральской школе по оптимальному управлению и дифференциальным играм Н.Н. Красовского [7, 8, 10]. Для построения оптимальной стратегии управления, используется метод экстремального сдвига [3, 6, 7, 10], предложенный автором [2].

Управляемый объект. Рассматривается объект, движение которого описывается обыкновенным векторным дифференциальным уравнением

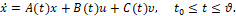(1)

Здесь x – n-мерный фазовый вектор управляемого объекта; t – время, моменты времени начальный t₀ и конечный ϑ зафиксированы; u– r-мерный вектор управления, υ– s-мерный вектор помехи. Точка над буквой обозначает производную по времени.

Вектор управления u и вектор помехи υ стеснены условиями

u∈P, υ∈Q, (2)

где P и Q – ограниченные замкнутые множества векторов, т.е. – компакты. Они определяют ресурсы соответственно управляющего органа U и органа V, вырабатывающего помехи в схеме управления по принципу обратной связи (рис.).

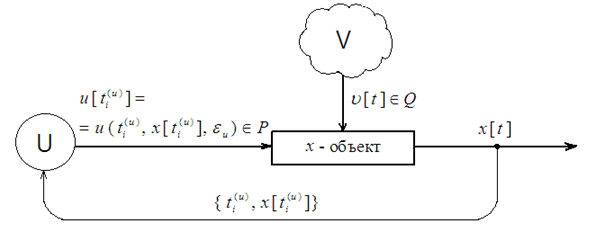
Рис. Схема управления по принципу обратной связи

Движение объекта (1), на отрезке времени [t_i, t_(i+1)]⊂[t₀, ϑ], которое обозначили символом   порождается некоторыми управлениями и помехами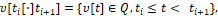    определены также как в работах [2, 3]. При этом в этих работах рассмотрена задача, когда информационным образом является позиция объекта {t_i,x[t_i]} и используется чистая позиционная стратегия  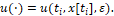 Здесь же, исходя их содержательного смысла рассматриваемой задачи управления при неполной информации не только о помехе, но и неточной запаздывающей информации о фазовых состояниях объекта, информационный образ, на базе которого будет формироваться стратегия управления, претерпевает существенные изменения. Он и будет играть ключевую роль в существовании оптимального решения рассматриваемой задачи.

Критерий качества процесса управления. Будем рассматривать критерий качества (критерий оптимальности) процесса управления γ следующего вида

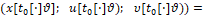
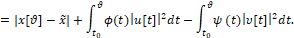 (3)

Здесь x ̃ – некоторый фиксированный n -мерный вектор – цель, к которой мы стремимся привести объект (1), (2) выбором управления u[t] по принципу обратной связи (рис.). В (3) интегральные слагаемые определяют затраты энергии на выработку управляющих воздействий и помех, где ϕ(t) и ψ(t) суть заданные кусочно-непрерывные функции времени
t, ϕ(t)≤α,  ψ(t)≤β, где α>0,  β>0 – заданные числа.

Информационный образ. Будем рассматривать такой случай, когда информация о состояниях x[t] идет с запаздыванием и еще, вообще говоря, с искажением. Текущую информацию при t≥t_0+h, где h>0 величина запаздывания, будем использовать в виде n-мерного вектора x* [t], где

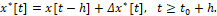(4)

Начальное фазовое состояние x[t₀]=x₀ объекта также сообщается с искажением. Обозначим

x₀*=x₀+Δx*₀. (5)

Целевое конечное фазовое состояние x ̃ также сообщается с искажением. Обозначим

x ̃^*=x ̃+Δx ̃^*. (6)

При этом величины x₀* (5) и x ̃* (6) сообщаются нам заранее. Полагаем, что они известны уже в некоторый момент t ̃₀<t_0, который уточним ниже. От момента времени t₀ до момента времени t_0+h управление 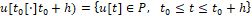 определяется лишь информацией об x₀* и x ̃*. Начиная с момента времени t_0+h, управление  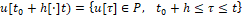определяется еще и информацией об x* [t] (1.11). При этом, несмотря на содержательный смысл величин x₀* и x* [t], вытекающий из (5), (6), не будем требовать, чтобы обязательно выполнялось равенство

x* [t_0+h]=x₀*.

Информационным образом (элементом) Υ[t₀] в начальный момент времени t=t₀ называется пара

Υ[t₀]={x₀*, x ̃*}. (7)

Информационным образом (элементом) Υ[t] при t≥t_0+h назовем совокупность компонент

 
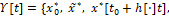
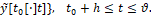(8)

При этом при t∈[t₀+h, ϑ] предполагается возможным запоминание истории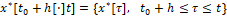  и реализации выработанного управления .

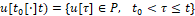В (8) y ̃[t₀ [⋅]t)={y ̃[τ],  t₀≤τ<t} – (n+1) - мерная вектор-функция, такая, что 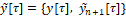 , где n-мерный вектор y складывается из первых n координат вектора y ̃.

Положим

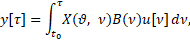(9)

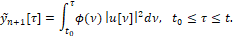 (10)

Согласно (9), (10), изменение во времени t переменных y[t]={y₁ [t],…,y_n [t]} и y ̃_(n+1) [t] описывается дифференциальными уравнениями

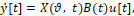(11)

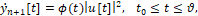(12)

с начальными условиями

y[t₀]={0,…,0},  y ̃_(n+1) [t₀]=0. (13)

Назовем допустимыми в (8) кусочно-непрерывные функции x* [⋅] и в (1.11), (1.12) – измеримые, ограниченные (каждая своей постоянной) функции u[⋅].

Итак, информационные элементы Υ[t] (9) и (10) определяют информационную Υ-систему.

Запаздывание информации. Следуя [5], поясним содержательный смысл запаздывания использования информации. Величина h не есть, вообще говоря, только время запаздывания подачи информации о состояниях x[τ] в орган управления. Величина h – это суммарное время, которое складывается из времени h^* запаздывания подачи информации в ЭВМ в органе управления, из времени h_* на подсчет в ЭВМ значения u[t] управляющего воздействия и из времени h ̃ передачи u[t] на x-объект. Итак,

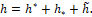
При этом полагаем

t_i-t_(i+1)≥h_*,  i=1,…, l-1,

где t_i=t_i^u и t_(i+1)=t_(i+1)^u – моменты из разбиения в схеме управления по принципу обратной связи (рис.).

Полагаем, что x₀* и x ̃* известны уже при t ̃₀=t₀-h-h_*. По постановке задачи полагаем, что в моменты времени 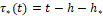 , 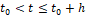по информации {x₀*, x ̃*} начинается подсчет величины

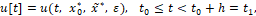
и эта величина вычисляется в течение времени 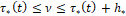 Таким образом, в частности, величина u[t₁ ] уже будет сосчитана в момент 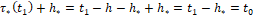. Полагаем, что в течение времени  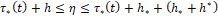вычисленное значение u[t] хранится в памяти. Затем за время 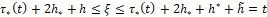вычисленное значение u[t] преобразуется в усилие u[t],  t₀<t≤t₁ на x-объект.  Разумеется, практически функция u[t],  t₀<t≤t₁ полагается кусочно-постоянной 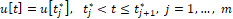с весьма малым шагом 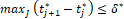, и, стало быть, практически вычисляются лишь значения .

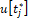В момент 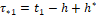в ЭВМ поступает новая информация

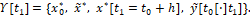
Заметим при этом, что в момент времени τ_*1=t₁-h+h* функцию y ̃[t₀ [⋅]t₁] мы полагаем уже известной, т.к., согласно предыдущему, подсчет определяющей ее функции 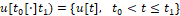 заканчивается в момент t₀, который наступает раньше, чем момент .

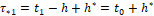По информации Υ[t₁] за время 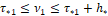 ЭВМ подсчитывает значение 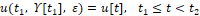, где t₁ и t₂ – моменты из разбиения Δ{t_i} (1.22), (1.34). Таким образом, вычисление величины u[t₂] заканчивается в момент 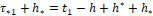. Затем в течение времени 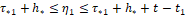сосчитанное значение u[t],  t₁<t≤t₂ хранится в памяти, и далее за время 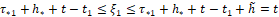сосчитанное значение u[t],  t₁<t≤t₂ преобразуется в управление u[t] на x-объект.

В момент 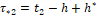поступает новая информация

.

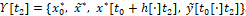При этом в момент τ_*2=t₂-h+h* функция y ̃[t₀ [⋅]t₂] полагается уже известной, т.к. подсчет в ЭВМ функции u[t₀ [⋅]t₂) заканчивается в момент 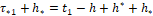и .

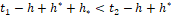Процесс продолжается по индукции по i. Пусть в момент τ_*i=t_i-h+h*, i=3,…, l-1 поступила информация

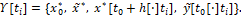
При этом предполагаем, что к моменту τ_*i функция y ̃[t₀ [⋅]t_i] уже сосчитана, т.е. уже сосчитана функция u[t₀ [⋅]t_i). В момент τ_*i по информации Υ[t_i] (1.37) начинается подсчет величины u[t],  t_i<t≤t_(i+1), который длится в течение времени 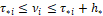 Таким образом, в момент 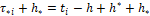заканчивается подсчет функции 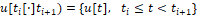. Далее в течение времени 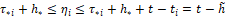сосчитанное значение u[t],  t_i≤t<t_(i+1) хранится в памяти, и затем за время 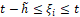оно преобразуется в управление u[t] на x-объект. При этом в момент τ_*i+1=t_i+1-h+h* можно снова начинать считать величину u[t],  t_i+1≤t<t_i+2. Для этого в момент τ_*i+1 необходимо иметь следующую информацию

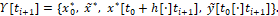
Такая информация в момент τ_*i+1 имеется. В самом деле, величина x* [t₀+h[⋅]t_i+1] становится известной в этот самый момент τ_*i+1, а функция y ̃[t₀ [⋅]t_(i+1)] становится известной в момент окончания вычисления функции u[t₀ [⋅]t_(i+1)], т.е. в момент 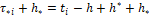, а с учетом (1.34) имеем .

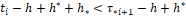Оптимальная стратегия. Назовем пару {t_i, Υ[t_i]}, состоящую из момента времени t_i и информационного образа Υ[t_i], информационной позицией Υ-системы в схеме управления по принципу обратной связи (рис., при замене 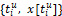 на).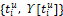

Для построения оптимальной чистой позиционной стратегии управления u⁰ (⋅)=u⁰ (t,Y,ε) используется метод экстремального сдвига на сопутствующие точки, изложенный в работах [2-6, 10].

Теорема. Построенная чистая позиционная стратегия управления u⁰ (⋅)=u⁰ (t,Y,ε) является оптимальной стратегией для рассматриваемой задачи конфликтного управления для линейной динамической системы (1) с критерием качества процесса управления γ (3).

Доказательство этого утверждения повторяет с понятными изменениями, связанными с заменой информационных образов, конструкции из работ [2-6, 10].