Режим установления колебаний в двумерной модели генератора обратной волны

Принцип действия электровакуумного прибора СВЧ диапазона – лампы обратной волны – основан на длительном взаимодействии замедленной электромагнитной и волны электронного потока. На основе этого свойства созданы генераторы электромагнитного излучения.

Основной задачей изучить сверхрегенеративный режим, при котором ток электронного потока больше пускового значения, и исследовать в линейном режиме процесс установления колебаний. Основной характеристикой является время переходного процесса.

Модель учитывает влияния фокусирующего магнитного поля конечной величины, дающее возможность возникновению поперечных высокочастотных (ВЧ) смещений электронов в пучке. Изучим как влияет ЭМП на процесс установления колебаний.

Распределим на несколько этапов установление колебаний [1-3].

В работах [1-3] подробно рассмотрена линейная одномерная теория лампы обратной волны (ЛОВ). Рассматривая базу развития теории, обратимся к двумерной модели. В работе [4] проанализированы результаты исследования нестационарной нелинейной теории ЛОВ.

1. Исходные соотношения

Электронный поток движется со средней скоростью v0 в продольном магнитном поле B(B,0,0) в направлении x. Уравнение движения и уравнение возбуждение в этом случае:

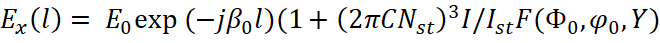
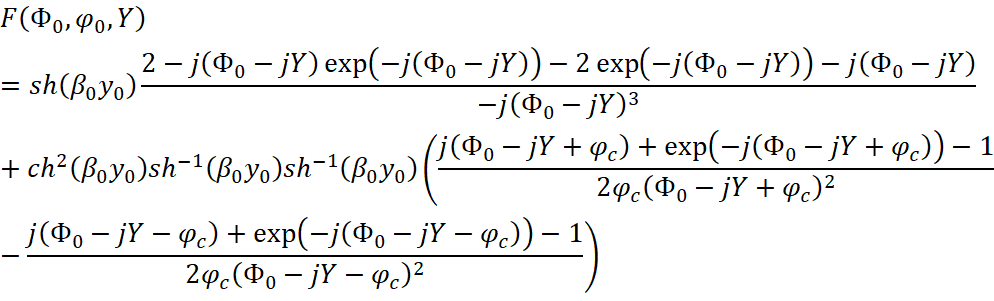
где  – ВЧ продольные и поперечные смещения электронов, η – удельный заряд электрона, сω= Bη – циклотронная частота, I0 – ток электронного потока, β0, – постоянные распространения волны в линии без электронного потока и с ним, d – ширина пространства взаимодействия, y0 – координата влета пучка, K0 – сопротивление связи.

Введение комплексной частоты ω1 =ω−jα по примеру [3] позволяет выделить параметр, отвечающий за нарастание α>0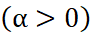 или затухание α<0 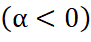колебаний во времени.

Колебания являются квазигармоническими в каждый момент времени, и их амплитуда за период изменяется на пренебрежимо малую величину. При пусковом значении тока и α= 0 колебания в системе являются чисто гармоническими и реализуется пусковой режим в ЛОВ.

Преобразования Лапласа при нулевых начальных позволяют найти:

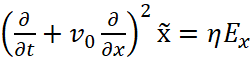
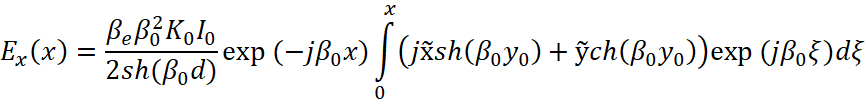
Если на входе в пространство взаимодействия пучок немодулированный и при x= l входной сигнал отсутствует, то определение параметров режима установления колебаний аналогично поиску пусковых условий генератора. Так определяется зависимость 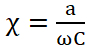 и времени установления колебаний от тока I0 и циклотронного угла пролета 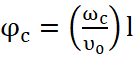, l – длина пространства. Введены  – относительный невозмущенный угол пролета, , u – скорость переноса энергии вдоль замедляющей системы, CNst – безразмерная пусковая длина, С – параметр усиления Пирса, I st – пусковое значение тока пучка.

2. Влияние магнитного поля на установление колебаний

Во всей рассматриваемой области χ>0 и колебания нарастают во времени по закону exp(αt) (рис. 1, а). С ростом φc и, соответственно, с ростом магнитного поля B, значения параметра χ снижаются за исключением значений от 3π до 4π, что связано с зависимостью пусковых условий от φc. Минимальное значение φc для расчетов равно 2π, т.к. в таких системах на практике меньшие значения магнитного поля не используются. Если φc>5π (величина магнитного поля, при котором поперечные смещения электронов можно не учитывать), построенные кривые стремятся к кривой, полученной в одномерном случае (рис. 1, б).

На рис. 2 приведены зависимости  при для случая без магнитного поля (а) и с учетом последнего (б). Величина 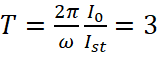 характеризует период колебаний. При отношении  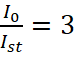для φ_c=2π величина t₃=175T, а при – φ_c=5π, а при –  и, t₃≈297T t₃≈339T соответственно. В [2, 3] также имеются численные оценки для времени t₃.

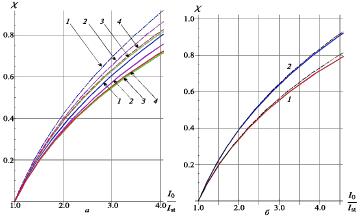
Рис. 1. Зависимости параметра χ от отношения I0Ist=2 (а) 1 – φс = 2π ,2–2.5π, 3–4π, 4–5π; сплошные кривые 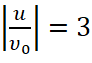, прерывистые  ; (б) 1 – , 2 – 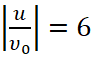, прерывистые линии – результаты одномерной теории, сплошные – результаты двумерной теории при φс = 5π (1) и φс =10π (2)

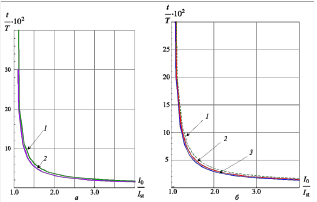
Рис. 2. Зависимости t3/T от отношения I0/Ist (а) φ_c=0, 1 – 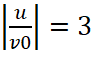, 2 – 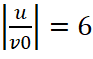; (б) 1 –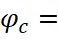 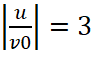  , 2 – φc=5π,  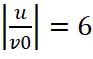3 – φc=2π,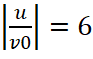

3. Частный случай

Если в электронном потоке возбуждается только медленная циклотронная волна (МЦВ), то все соотношения существенно упрощаются, т.к. в них следует положить Ф0=φ_c, что является необходимым условием для циклотронного резонанса.

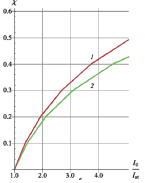
Рис. 3. Зависимости параметра χ от отношения I0/Ist для φc=5π, 1 – 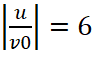, 2 –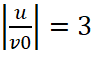

Из рис. 1а и рис.3 видно, что параметр χ принимает меньшие значения в последнем случае, что соответствует меньшей скорости нарастания колебаний в системе.

Данные результаты пригодны только в случае циклотронного резонанса вдали от пусковых условий ЛОВ, полученных в рамках общего подхода. Рассмотрен процесс установления колебаний в генераторе обратной волны в сверхрегенеративном режиме с введением комплексной частоты. С ростом φc параметр, отвечающий за нарастание колебаний в системе со временем, снижается (за исключением значений от 3π до 4π - см. рис. 1, а (кривые 3, 4)). Проведена оценка времени установления колебаний при различных значениях магнитного поля.