Математическая управляемая модель криволинейного движения трактора с прицепом

Введение. В работе конструируется некоторая модель управляемого движения трактора с прицепом по криволинейной траектории (окружности). /В соответствии с известной теорией достаточно сложные нелинейные дифференциальные уравнения линеаризуются и рассматриваются малые движения системы. Рассматривается случай, когда центр тяжести трактора двигается по окружности с постоянной скоростью. Это определяет граничные условия для решения уравнений на фиксированном отрезке времени. В рассмотренном случае малых движений системы найденный управляющий момент обеспечивает требуемое движение и исходной нелинейной управляемой систему, моделирующей в первом приближении движение трактора с прицепом. Одним из существенных моментов при составлении рассматриваемой упрощенной математической модели процесса движения тракторного поезда по окружности является то, что должно выполняться условие - центр тяжести ведущего трактора должен двигаться по окружности заданного радиуса с постоянной скоростью. В рассматриваемой модели в качестве обобщенных координат, определяющих положение звеньев маятника, являются углы. В случае большого отрезка времени движения тракторного поезда по окружности этот отрезок разбивается на малые интервалы и конечное положение системы на одном отрезке является начальным положением система на следующем отрезке времени. Предлагаемая конструкция допускает эффективное компьютерное моделирование движения системы «трактор-прицеп» в реальном масштабе времени. Работа продолжает исследования авторов по задачам математического моделирования [1, 2].

Движение объекта. Рассматривается криволинейное движение транспортно-погрузочного средства, состоящего из трактора с прицепом (рис. 1).

Рис. 1. Трактор с прицепом

При этом расчетная схема (модель) для такой системы имеет следующий вид (рис. 2).

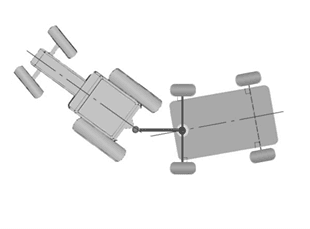
Рис. 2. Расчётная схема (модель)

В данной работе рассматривается упрощенная модель (рис. 3).

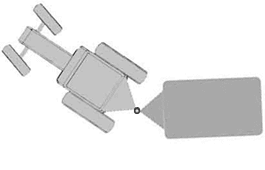
Рис. 3. Упрощённая модель

Тогда в качестве расчетной схемы выбирается двухзвенная маятниковая система, состоящая из двух стержней соединенных цилиндрическим шарниром, двигающаяся в горизонтальной плоскости.       При этом устойчивое движение второго стержня (прицепа) по окружности обеспечивается выбором подходящего управляющего момента М_УПР в цилиндрическом шарнире (в точке О), соединяющем звенья системы. Рассматривается случай, когда центр тяжести трактора – точка С_ТР двигается по окружности с постоянной скоростью.

Уравнения движения. Для составления математической модели, т.е. описания движения системы с помощью дифференциальных уравнений [1], используется основной аппарат моделирования движения механических систем с тем или иным количеством степеней свободы – уравнения Лагранжа второго рода [3]. В рассматриваемом случае система имеет две степени свободы, поэтому в качестве обобщенных координат выбираем два угла ϕ и ψ (рис. 4).

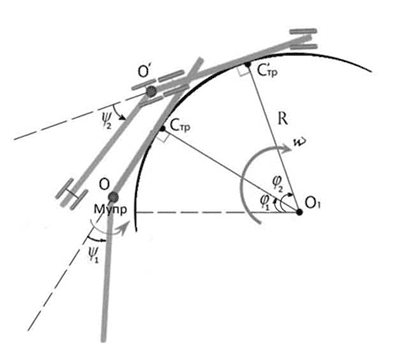
Рис. 4. Обобщённые координаты

Уравнения Лагранжа второго рода принимают следующий вид:

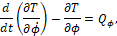  (1)

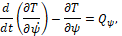(2)

где Т – кинетическая энергия системы, которая через параметры трактора (первого стержня) и прицепа (второго стержня) выражается в следующем виде:

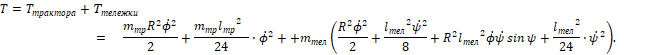(3)

В уравнения (1) и (2)  и  суть обобщенные силы, которые в рассматриваемом случае имеют вид:

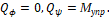  (4)

Рассматривая малые колебания (движения) [3] двухзвенной маятниковой системы (рис. 4), линеаризуем, получаемые в процессе дифференцирования левых частей уравнений (1) и (2), достаточно сложные нелинейные дифференциальные уравнения движения известным методом [2] и приводим их к виду:

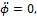  (5)

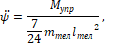  (6)

где две точки над буквой обозначают вторые производные по времени.

Полученную систему дифференциальных уравнений мы называем упрощенной управляемой математической моделью криволинейного движения тракторного поезда, изображенного на рис. 1. При этом из уравнения (5) следует, что мы рассматриваем такой случай, когда центр тяжести С_ТР трактора двигается по окружности с постоянной скоростью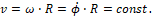 

Задаваясь начальными условиями:

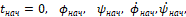  (7)

интегрируем два раза дифференциальные уравнения (5) и (6) получаем следующие законы движения системы:

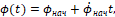 (8)

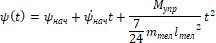  (9)

на отрезке времени:

t_нач = 0 ≤ t ≤ t_кон  (10)

Чтобы обеспечить устойчивое движение (следование) прицепа за трактором на малом отрезке времени (9) задаемся требуемыми (например, исключающим складывание как «ножа» прицепа и трактора – второго звена маятника с первым) граничными условиями в момент времени :

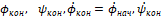   (11)

Искомый управляющий момент имеет следующий вид:

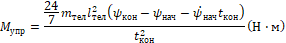  (12)

Построенное управление (в виде управляющего момента (12)) обеспечивает перемещение системы (5), (6) из заданного начального (7) в требуемое конечное (11) положение за заданное время (10). При этом, в соответствии с принципом малых колебаний системы [2], найденный управляющий момент (12) обеспечивает и указанное перемещение исходной нелинейной системы, получаемой в виде уравнений Лагранжа второго рода (1), (2) без линеаризации последних.

Благодарности. Авторы благодарят магистранта Брагина Кирилла за помощь в выполнении графических рисунков для статьи.