В производство несущих каркасов произошло внедрение высокопрочного бетона, что привело к использованию конструкций из сжатых колонн, так как они обладали меньшими размерами поперечных сечений по сравнению с обычными бетонными секциями. Потери устойчивости возрастает, при увеличении гибкости, а также колонны изначально изгибаются в плоскости эксцентриситета или плоской деформации. Гибкость увеличивается, поэтому возможность потери устойчивости возрастает, когда колонны изначально изгибаются в плоскости эксцентриситета или плоской деформации. Поэтому возрастает важность совершенствования метода проверки колонн.
Существует два случая работы внецентренно сжатых элементов (рис.1). Основное отличие между ними заключается в следующем: в первом случае относительная высота сжатой зоны бетона, меньше граничного значения, сечение сжато частично, когда большая его часть растянута. В этом случае арматура А, растянута, а вторая арматура А' сжата этот случай называют случаем больших эксцентриситетов.
Во втором случае большая часть или все сечение колонны сжаты, и тогда при сравнении с первым случаем меняется характер работы арматуры: напряжения в арматуре А, расчетные значения сопротивления арматуры не достигаются, и она может быть либо слабо сжата, либо слабо растянута этот случай называют случай малых эксцентриситетов.
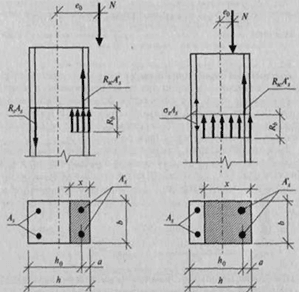
Рис. 1. Два случая работы внецентренно сжатых элементов
Сжатые бетонные элементы очень сложно поддаются центральному сжатию, например, несовершенные геометрические формы колонн, характеристики несущих конструкций, недостаточная точность регулировки арматуры, неоднородность бетона и другие факторы. Приводит это к тому, что практически все сжатые бетонные элементы можно считать сжатыми отдельно. Нагрузка, под которой находится вертикальный стержень (рис. 2), потерянная устойчивость зависит лишь от момента инерции участка I и от модуля Юнга. Данный стержень не разрушается при образовании выпуклости. Он изгибается так, чтобы он "выскользнул" из-под нагружаемой силы. Если "предел упругости" материала не был достигнут во время нагружения, то после снятия нагрузки стержень снова выпрямится.
Рис. 2. Действие силы F на стержень
Применяемость изобретенного Эйлером математического метода вариационного исчисления при возможности определении наименьшей высоты тонкого вертикального стержня, при которой этот стержень начинает выпучиваться под собственным весом, привело к получению формулы Эйлера
Формула Эйлера применима в некоторых случаях, когда гибкость стержня превосходит или равна предельной гибкости. В тех случаях, когда гибкость стержней меньше предельной, формулу Эйлера нельзя применить и пользуются эмпирической формулой Ясинского.
В дальнейшем, множественные исследования Ф.С. Ясинского и других многих ученых показали, что среди упругопластических деформаций формула Эйлера не может быть применима. Именно поэтому использование на практике может быть только в некоторых случаях, когда при гибкостях λ, которые превышают критическую величину λcr, когда связь между напряжениями и деформациями во всех материалах конструкции можно считать пропорциональной. Производится оценивание несущей способности сжатых элементов различной гибкости по условиям прочности и устойчивости, а также для железобетонных колонн, которые были испытаны Бабичем С.В. и Астафьевым Д.О. при гибкостях λ = 93 и λ = 78. Итоги сравнения экспериментальных данных с результатами аналитического расчета, которые были получены по данной методике, показали некоторые малочисленные расхождения, что допускает возможность ее применения при решении поверочных и проектировочных задач [5, c. 41].
Расчет бетонных и железобетонных конструкций по деформациям должен производиться из условия, по которому прогибы, углы поворота, перемещения и амплитуды колебания конструкций от многочисленных воздействий не должны превышать соответствующих им предельно допустимых значений [4, c. 28].
Расчет внецентренно сжатых колонн производят с учетом их работы в системе поперечного каркаса здания. Наряду со множеством достоинств большинства разработанных методик, которые могут позволять оценивать напряженное состояние железобетонного элемента во всех стадиях нагружения, также присутствует и недостаток: почти все отмеченные методики были созданы применительно к расчету изгибаемых и внецентренно сжатых железобетонных элементов малой гибкости. В гибких железобетонных вертикальных стержнях, несущая способность которых находится в прямой зависимости от величины деформаций [2, c. 23].
Для надежного и точного использования различных методик расчета, которые должны учитывать фактические диаграммы деформирования бетона, нужно располагать аналитическими зависимостями между напряжениями и деформациями бетона. Сегодня таких зависимостей большое множество, но все же предпочтение отдается диаграммам, которые отражают реальную работу бетона под нагрузкой, и при этом отличающимися простотой записи и легкостью выполнения операций интегрирования и дифференцирования. Вопрос расчета гибких внецентренно сжатых элементов исследован весьма глубоко, но все же прямого сопоставления результатов по различным методам не было найдено в доступных источниках. Системное подтверждение расчетных методик на основе испытаний и сопоставление результатов с популярными расчетами по недеформированной схеме представляют очень важную задачу для всей практики проектирования [3, c. 13].

.png&w=640&q=75)