Об одной задаче оптимального управления в классе смешанных стратегий

Введение. В работе рассматривается задача конфликтного управления одни конкретным динамическим объектом – материальной точкой на горизонтальной плоскости. Орган управления состоит из некоторой установки способной создавать в каждый момент времени одно из четырех взаимно перпендикулярных управляющих воздействий (сил). В качестве неконтролируемой помехи рассматривается люфт (угол поворота) рассматриваемой установки. В этом случае движение объекта (точки) описывается дифференциальным уравнением в форме второго закона Ньютона и в нормальной форме векторным нелинейным по управлению и помехе дифференциальным уравнением. Критерий качества процесса управления – расстояние от точки на плоскости в конечный момент времени до заданного центра (начала координат). Так как для конфликтно-управляемой динамической системы не выполняется так называемое условие седловой точки для маленькой игры [8] эффективное решение задачи приводится в классе смешанных стратегий [2, 10], т.е. используется некоторый вероятностный механизм формирования управления. При этом окончательный гарантированный результат управления гарантируется с вероятностью сколь угодно близкой к единице. Задача на минимакс выбранного критерия качества решается в рамках концепции, разрабатываемой в уральской школе по оптимальному управлению и дифференциальным играм Н.Н. Красовского [5, 7, 10] и решается методом экстремального сдвига на сопутствующие точки, предложенным автором [3].

Движение объекта. Рассматривается объект (материальная точка М), двигающийся в горизонтальной плоскости в декартовой системе координат {q₁, q₂}  под действием силы k[t] (рис. 1), описываемый векторным нелинейным дифференциальным уравнение в форме второго закона Ньютона

,

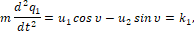
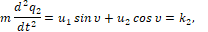
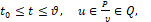  (1)

где u₁, u₂ – суть проекции вектора силы управления u на оси q₁, q₂ (рис. 1), υ – помеха – угол люфта управляющей силы, t – время, начальный и конечный моменты времени t₀ и ϑ зафиксированы, P и Q – соответственно множества векторов u и углов , определяющие ресурсы органа управления U и органа V, вырабатывающего помехи. Пусть в данном конкретном примере множества P и Q определены следующим образом.

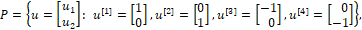
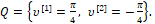    (2)

Т.е. содержательно орган управления U можно трактовать как некоторое устройство из четырех взаимно перпендикулярных двигателей (рис.2) и каждый из двигателей может создавать тягу, равную единице. Такие конструкции (навигационные устройства) устанавливались, например, на посадочных модулях Аполлонов для корректировки их посадки на поверхность Луны (рис. 3).

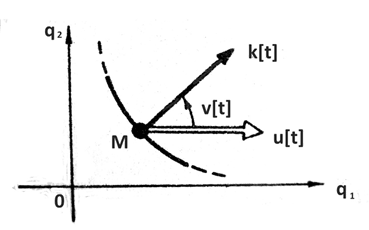
Рис. 1. Движение объекта

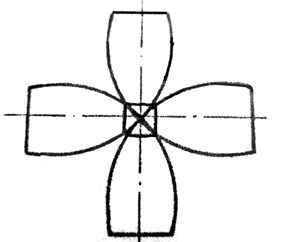
Рис. 2. Орган управления

Рис. 3. Навигационные устройства в космосе

При этом последовательным включением двигателей (они были установлены с четырех сторон посадочного модуля) управлял не человек, а бортовой компьютер в программу которого был заложен некоторый алгоритм. Целью управления было привести посадочный модуль в заданную точку поверхности Луны. Как известно у Аполлона 11 таким модулем был Орёл (рис. 4) и его успешно посадили в так называемое море Спокойствия. Однако здесь мы рассматриваем некоторый усложненный случай, когда крестообразный орган управления имеет некоторый люфт, определяемый множеством Q (2) (рис. 5).

Рис. 4. Посадочный модуль Орёл Аполлона 11

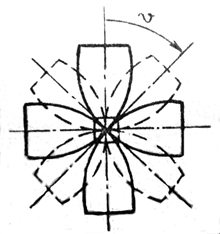
Рис. 5. Люфт управляющего органа

 Показатель качества. Цель управления – минимизировать расстояние от точки М в конечный момент времени функционала t=ϑ некоторого центра О (рис.1). Тогда показатель (критерий) качества процесса управления задаётся в виде функционала γ от движения q[t₀ [⋅]ϑ]={q[t], t₀≤t≤ϑ} объекта (1)

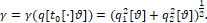 (3)

Смешанная стратегия. Будем рассматривать задачу о выборе управлений  помех , соответственно минимизирующих и максимизирующих критерий качества  (3). В рассматриваемом случае для объекта (2) не выполняется условие седловой точки для маленькой игры [8] т.е. – равенство 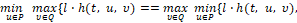 для любого вектора l∈R⁴. Известно, что в этом случае задача эффективно решается в классе, так называемых, смешанных стратегий [2, 10]. При этом используется некоторый вероятностный механизм для конструирования управлений

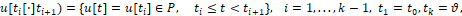
где P – набор из четырёх единичных, взаимно перпендикулярных управляющих векторов (2).

Оптимальная смешанная стратегия существует [2, 10]. При этом для её построения используются два метода – метод экстремального сдвига на сопутствующие точки, предложенный автором [3, 4, 10] и метод взаимного устойчивого отслеживания движении реального объекта (1) и его виртуальной модели-поводыря [5, 10].

Численный эксперимент. Приведем результаты соответствующего управляемого процесса при неконтролируемой помехе – люфте управляющего органа U (рис. 5). Были выбраны параметры – точка стартовала из исходного состояния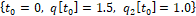 при следующем разбиении отрезка времени управления в схеме обратной связи [ ]

t_i+1=t_i+δ,  i=1,...,k-1, t₁=t₀=0, t_k=ϑ=2, δ=0.005.

На рис. 6 приведено движение точки М (рис.1) при оптимальном способе управления и следующем способе формирования помехи. В каждый момент времени с вероятностью 1/2 может случиться

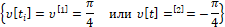
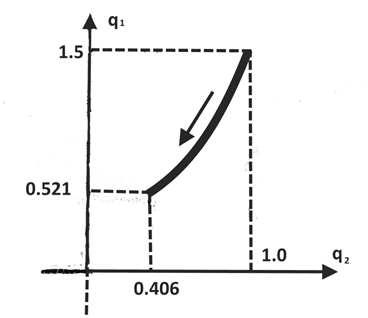
Рис. 6. Траектория движения 1

Здесь получили

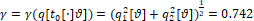    (4)

На рис. 7 приведено движение точки М (рис.1) при оптимальном способе формирования помехи и следующем способе формирования управления. В каждый момент времени с вероятностью 1/4 может случиться

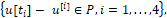
где Р – множество единичных векторов (2).

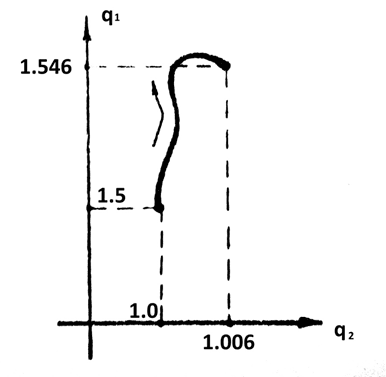
Рис. 7. Траектория движения 2

Здесь получили

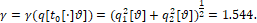  (5)

Движения (рис.6,7) получились в результате численных экспериментов, проведенных автором статьи на ЭВМ ВАКС (VAX) 11/750 в Университете города Сараево (Босния и Герцеговина).

Как видно при оптимальном способе управления точка ближе приближается к началу координат, что хорошо согласуется с теорией дифференциальных игр [1-10].