На процессы, происходящие в любой области деятельности человека, будь то производство, сельское хозяйство, строительство или образование, влияет много факторов. Для исследования процессов по определенным параметрам отбираются некоторые наиболее активные. Рассмотрим область образовательной деятельности и такое актуальное направление, как повышение качества знаний учащихся, которое можно охарактеризовать с помощью уровня успеваемости. В свою очередь, уровень успеваемости зависит от множества факторов. Например, от методики преподавания дисциплины, от посещения студентами занятий, от уровня знаний самих учащихся, от перехода на дистанционное обучение, от периодичности проверок знаний и т. п. [2, c. 360]. Одной из существенных проблем современного образования является проблема неуспеваемости. Мотивировать обучаемых к получению знаний, изучению предметов и, соответственно, лучшей подготовке их, как специалистов, – задача первостепенная. Для этого проводится анализ состояния процесса обучения с помощью исследования уровня успеваемости – одного из самых важных этапов как процесса повышения качества обучения, так и всего процесса обучения в целом.
Для прогнозирования успеваемости обучаемых построим линейную модель множественной регрессии на основе математических методов планирования [4, с. 23]. В качестве входных параметров возьмем такие характеристики учебного процесса, как посещаемость занятий обучаемыми и частоту опросов их знаний в течение одного семестра, в качестве выходного параметра – уровень успеваемости. Провести исследование влияния посещаемости занятий студентами и количество проверок их знаний на уровень успеваемости предлагается с помощью применения методов планирования эксперимента. Самым простым центральным и линейно-ортогональным планом является двухуровневый план полного факторного эксперимента ПФЭ2n. В нашем случае используются два фактора, поэтому будем рассматривать двухуровневый план двухфакторного эксперимента (ПФЭ22) [3, c. 62-65].
Оптимальные соотношения посещаемости занятий студентами и количество опросов их знаний в течение семестра для процесса прогнозирования уровня успеваемости получены в ходе планирования двухуровневого плана факторного эксперимента (ПФЭ22) [3, с. 78]. Итак, посещаемость студентов в семестре должна меняться в диапазоне от 91 до 97%, а частота проверок знаний обучаемых в семестре – от 6 до 10 раз.
Посещаемость в % (Х1) и количество опросов в семестре в единицах (Х2) – это варьируемые независимые переменные или факторы плана ПФЭ22.
Основной уровень и интервалы варьирования независимых переменных: для Х1 – это 94 и 3, для Х2 – это 8 и 2.
Матрица планирования эксперимента Х для плана ПФЭ22 в безразмерном выражении величин факторов представляет собой:
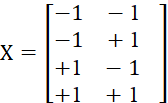 , (1)
, (1)
Факторы на нижнем уровне характеризуются значением –1, на верхнем уровне +1 [6, с. 116-118]. План предусматривает четыре опыта – число сочетаний из 2 переменных при их изменениях на 2 уровнях.
В качестве зависимой переменной y рассматривается средняя оценка успеваемости студентов в семестре по специальным дисциплинам, которая вычисляется исходя из результатов опросов студентов. Учитываются три специальные дисциплины (3 значения по y).
Уравнение по результатам опытов двухфакторного эксперимента включает оценки четырех коэффициентов (линейные коэффициенты уравнения и коэффициент, учитывающий эффект парного межфакторного взаимодействия) и является итогом реализации плана ПФЭ22.
Итак, уравнение регрессии, полученное для процесса прогнозирования среднего уровня успеваемости в течение семестра учебного процесса при таких варьируемых величинах, как посещаемость занятий и количество проверок знаний, имеет следующий вид:
![]() , (2)
, (2)
Коэффициент парного межфакторного взаимодействия а12 исключается из уравнения, так как он незначимый – его значение -0,01 меньше значения доверительного интервала 0,1198. Влияние этого коэффициента на отклик ничтожно.
Полученные линейные коэффициенты в уравнении регрессии (2) сполна характеризуют влияние изучаемых факторов на исследуемый процесс. Например, увеличение количества проверок знаний в семестре (х2) до 10 раз вызывает повышение среднего уровня успеваемости (y) на 0,13 – на значение коэффициента при этой переменной. Из уравнения регрессии следует, что на повышение успеваемости большее влияние оказывает количество опросов студентов, чем посещаемость занятий ими.
Табличное значение критерия Фишера для параметров исследуемого процесса больше вычисленного Fт > F (5,32 > 4,954). Значит уравнение регрессии адекватно описывает экспериментальные данные. Проверим, является ли полученное уравнение хорошей математической моделью, описывающей рассматриваемый процесс. Для этого установим, работает ли уравнение в центре эксперимента [6, с. 121]. Проведем оценку описания внутренней области изучаемого факторного пространства. Сравним доверительную ошибку, определенную по критерию Стьюдента (0,26), с разницей между свободным членом и среднеарифметической оценкой дополнительного опыта в центре эксперимента (0,09). Видно, что невязка в центре эксперимента меньше доверительной ошибки невязки (0,09<0,26), значит линейное уравнение регрессии правильно характеризует внутреннюю область изучаемого факторного пространства. Следовательно, полученное уравнение можно считать хорошей математической моделью исследуемого процесса, так как оно работоспособно (0,26>0,09) и адекватно (5,32>4,954).
Графическая интерпретация исследуемой зависимости представлена ниже (рис. 1, 2).
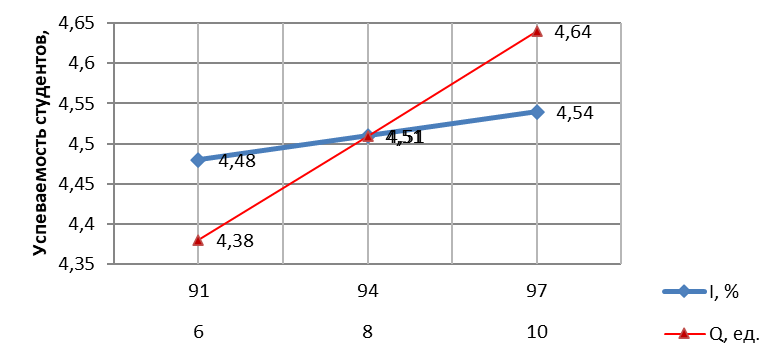
Рис. 1. Зависимость успеваемости студентов от посещаемости занятий (I) и контроля знаний (частоты опросов Q)
Посещаемость обучаемых мало влияет на величину успеваемости. При изменении процента посещаемости успеваемость меняется, но незначительно (0,03). Несомненно, большее влияние на результат оказывает частота проверки знаний. Диапазон значений успеваемости при изменении количества опросов более обширен (от 4,38 до 4,64). При увеличении количества опросов явно наблюдается значительный рост среднего показателя уровня успеваемости.
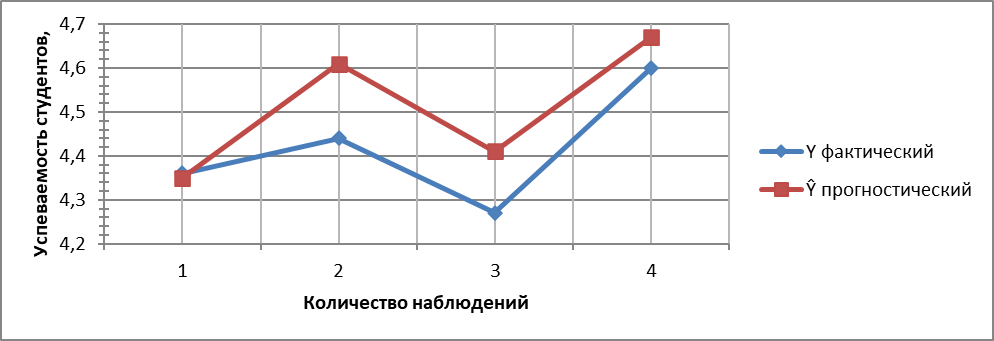
Рис. 2. Прогностический и фактический средний уровень успеваемости
Прогностические значения успеваемости, полученные в результате проведенного эксперимента (ПФЭ22 – 4 опыта и 4 коэффициента), ненамного отличаются от фактических показателей средней успеваемости. Максимальная погрешность вычислений составляет всего 3,2%, что говорит о целесообразности проведенных исследований.
Построен двухуровневый план полного двухфакторного эксперимента для исследования уровня успеваемости за семестр по трем дисциплинам в зависимости от таких характеристик учебного процесса, как посещение занятий учащимися и количество проводимых преподавателем опросов их знаний.
Для анализируемого процесса разработано уравнение регрессии первого порядка. Обоснована адекватность уравнения.
На основе полученных данных и аналитических зависимостей составлена математическая модель, описывающая процесс прогнозирования влияния посещаемости занятий студентами и количество проверок их знаний на уровень успеваемости. Исследуемый процесс наглядно интерпретируют графические зависимости.
По итогу проведенного исследования и анализа зависимости уровня успеваемости от посещаемости и количества опросов можно сделать следующий вывод: на успеваемость студентов существенное влияние оказывает частота проверок их знаний. Поэтому необходимо постоянно или как можно чаще осуществлять контроль знаний обучаемых, ведь от этого не в малой степени зависит и повышение эффективности самого учебного процесса [5, с. 225].
Использование статистических методов анализа совместно с методами планирования эксперимента позволяет построить наиболее содержательную модель процессов исследований в образовательной деятельности, позволяет определить степень влияния тех или иных заданных факторов на результат с помощью коэффициентов уравнений регрессии [1, с. 146]. А целью исследований как раз и является выявление факторов, максимально повышающих качество знаний студентов.
Математические модели двухфакторного процесса с независимыми оценками эффекта влияния фактора на величину критерия оптимальности привлекают своей простотой и применяются достаточно часто [3, c. 70].

.png&w=640&q=75)