Задача 1. Вариант 1 (Заключительный этап, 8 класс, 20 баллов)
В равнобедренной трапеции ![]()
![]() больше
больше ![]() на стороне
на стороне ![]() взяли точку
взяли точку ![]() и провели через нее прямую параллельную
и провели через нее прямую параллельную ![]() до пересечения с
до пересечения с ![]() в точке
в точке ![]() так, что
так, что ![]() Площадь полученного отсеченного треугольника
Площадь полученного отсеченного треугольника ![]() оказалась равной
оказалась равной ![]() . Найти площадь трапеции
. Найти площадь трапеции ![]() если
если ![]() и
и ![]()
Решение
1) Пусть ![]() так как
так как ![]() то
то ![]() и
и ![]() - равнобедренная трапеция (по условию
- равнобедренная трапеция (по условию ![]() ),
), ![]() .
.
2) Проведем ![]() тогда
тогда ![]()
![]() Следовательно,
Следовательно, ![]() (по двум углам) и
(по двум углам) и 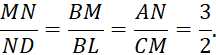 Обозначим
Обозначим ![]()
![]() (рис. 1).
(рис. 1).
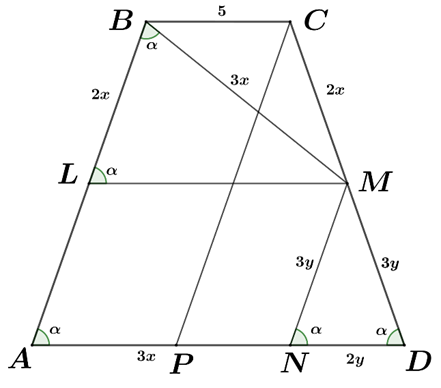
Рис. 1
3) Обозначим ![]()
![]() Тогда
Тогда 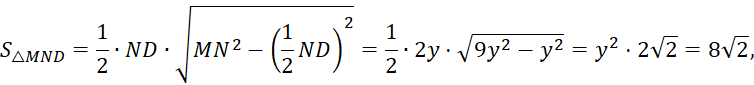
![]() следовательно,
следовательно, ![]()
![]()
4) Проведем ![]() тогда
тогда ![]()
![]() . По теореме Фалеса
. По теореме Фалеса 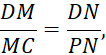
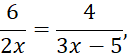 получаем
получаем ![]()
5) По условию ![]()
![]() Найдем высоту
Найдем высоту ![]() трапеции
трапеции ![]()
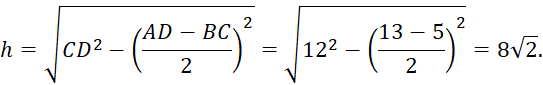 Площадь трапеции
Площадь трапеции ![]() равна:
равна: 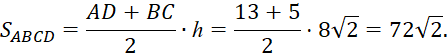 Критерии выставления баллов представлены в таблице 1.
Критерии выставления баллов представлены в таблице 1.
Ответ: ![]() .
.
Таблица 1
Баллы | Критерии выставления баллов |
20 | Решение верно. |
15 | Решение верно, но недостаточно обоснованно или допущена одна арифметическая ошибка, или найдены все стороны трапеции, но задача не доведена до конца. |
10 | Доказано равенство углов и подобие треугольников. |
5 | Доказано одно из утверждений, ведущих к решению задачи. |
0 | Решение не верно или отсутствует. |
Задача 1. Вариант 2 (Заключительный этап, 8 класс, 20 баллов)
В равнобедренной трапеции ![]()
![]() больше
больше ![]() на стороне
на стороне ![]() взяли точку
взяли точку ![]() и провели через нее прямую параллельную
и провели через нее прямую параллельную ![]() до пересечения с
до пересечения с ![]() в точке
в точке ![]() так, что
так, что ![]() Площадь полученного отсеченного треугольника
Площадь полученного отсеченного треугольника ![]() оказалась равной
оказалась равной ![]() . Найти площадь трапеции
. Найти площадь трапеции ![]() если
если ![]() и
и ![]()
Ответ: ![]() .
.
Задача 2. Вариант 1 (Заключительный этап, 8 класс, 15 баллов)
Решите уравнение:
![]()
Решение
Сделаем замену переменной ![]() и решим полученное уравнение:
и решим полученное уравнение:
![]()
![]()
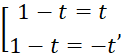
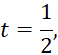
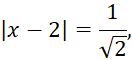
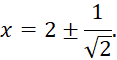
Критерии выставления баллов представлены в таблице 2.
Ответ: 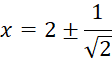 .
.
Таблица 2
Баллы | Критерии выставления баллов |
15 | Решение верно. |
10 | Ход решения верный, но допущена одна арифметическая ошибка. |
5 | Сделана замена переменной, но есть ошибки в применении формул или раскрытии модуля. |
Задача 2. Вариант 2 (Заключительный этап, 8 класс, 15 баллов)
Решите уравнение:
![]()
Ответ: ![]() .
.
Задача 3 (Заключительный этап, 8 класс, 15 баллов)
Найдите все такие значения параметра ![]() что уравнение имеет только одно решение.
что уравнение имеет только одно решение.
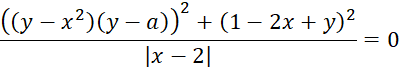
Решение
Уравнение равносильно системе:
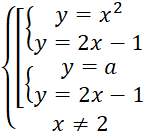 ,
,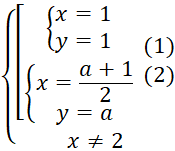
Выясним при каких значениях параметра эта система имеет единственное решение. Если 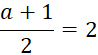 или
или ![]() то (в силу ограничения для переменной
то (в силу ограничения для переменной ![]() ) система имеет только одно решение (1;1). Если
) система имеет только одно решение (1;1). Если 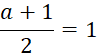 или
или ![]() то решения систем (1) и (2) совпадают, следовательно, система снова имеет единственное решение (1;1). При
то решения систем (1) и (2) совпадают, следовательно, система снова имеет единственное решение (1;1). При ![]()
![]() решения систем(1) и (2) существуют, различны и уравнение имеет два различных решения. Следовательно, уравнение имеет только одно решение тогда и только тогда, когда
решения систем(1) и (2) существуют, различны и уравнение имеет два различных решения. Следовательно, уравнение имеет только одно решение тогда и только тогда, когда ![]() Критерии выставления баллов представлены в таблице 3.
Критерии выставления баллов представлены в таблице 3.
Ответ: 1; 3.
Таблица 3
Баллы | Критерии выставления баллов |
15 | Верное обоснованное решение |
10 | Верный ход решения, но не рассмотрен случай совпадения решений при либо допущена вычислительная ошибка. |
5 | Верные шаги по упрощению уравнения (например, уравнение сведено к совокупности, системе), но не рассмотрено |
Задача 4. Вариант 1 (Отборочный (заочный) онлайн-этап, 9 класс, 14 баллов)
Дано четное число ![]() не оканчивающееся на 0. Найти предпоследнюю цифру числа
не оканчивающееся на 0. Найти предпоследнюю цифру числа ![]()
Решение
Найдем две последние цифры числа ![]() Так как
Так как ![]() – четное число и некратно 10, то оно может иметь вид
– четное число и некратно 10, то оно может иметь вид ![]() или
или ![]() (то есть не
(то есть не ![]() ), где
), где ![]() – некоторое натуральное число.
– некоторое натуральное число.
Используя бином Ньютона (или перемножая скобки и используя свойства сравнений), получим, что ![]() . Аналогично,
. Аналогично, ![]() . Далее,
. Далее, ![]() поэтому
поэтому ![]() . Таким образом, в любом случае
. Таким образом, в любом случае ![]()
Следовательно, возможны только четыре варианта двух последних цифр числа ![]() : 01, 26, 51, 76 следует, что
: 01, 26, 51, 76 следует, что ![]() делится на 4, поэтому возможен только вариант 76, то есть предпоследняя цифра числа
делится на 4, поэтому возможен только вариант 76, то есть предпоследняя цифра числа ![]() – это
– это
Ответ: 7.
Задача 4. Вариант 2 (Отборочный (заочный) онлайн-этап, 9 класс, 14 баллов)
Дано четное число ![]() не оканчивающееся на 0. Найти предпоследнюю цифру числа
не оканчивающееся на 0. Найти предпоследнюю цифру числа ![]()
Ответ: 7.
Задача 5. Вариант 1 (Отборочный (заочный) онлайн-этап, 9 класс, 14 баллов)
На каждой из 61 карточки написано одно из чисел: 3, 4 или 5. Число карточек с тройками на 11 больше карточек с пятерками. Из этих карточек, располагая одну карточку за другой, составляют натуральное число ![]() Найдите остаток от деления числа
Найдите остаток от деления числа ![]() на 9.
на 9.
Решение
1. Остаток от деления натурального числа на ![]() 9 равен остатку от деления на 9 суммы цифр этого числа.
9 равен остатку от деления на 9 суммы цифр этого числа.
2. Пусть ![]() – число троек среди цифр числа
– число троек среди цифр числа ![]()
![]() – число четверок,
– число четверок, ![]() – число пятерок. Из условия
– число пятерок. Из условия 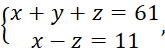
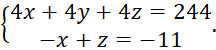 Сложив уравнения системы, получим
Сложив уравнения системы, получим ![]() то есть сумма цифр числа
то есть сумма цифр числа ![]() равна
равна ![]() ,
, ![]() следовательно, остаток от деления на 9 суммы цифр числа
следовательно, остаток от деления на 9 суммы цифр числа ![]() равен 8.
равен 8.
Ответ: 8.
Задача 5. Вариант 2 (Отборочный (заочный) онлайн-этап, 9 класс, 14 баллов)
На каждой из 45 карточек написано одно из чисел: 4, 5 или 6. Число карточек с четверками на 5 больше карточек с шестерками. Из этих карточек, располагая одну карточку за другой, составляют натуральное число ![]() . Найдите остаток от деления числа
. Найдите остаток от деления числа ![]() на 9.
на 9.
Ответ: 4
Задача 6. Вариант 1 (Отборочный (заочный) онлайн-этап, 10 класс, 9 баллов)
Найти наибольшее значение выражения:
![]()
при ![]() и
и ![]()
Решение
Обозначим наше выражение:
![]()
Выясним при каких ![]() оно определено:
оно определено: 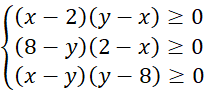 , перемножив неравенства системы, получим следствие системы
, перемножив неравенства системы, получим следствие системы ![]() или
или 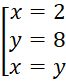 . Уточним область определения выражения
. Уточним область определения выражения ![]()
Если ![]() , то система сводится к неравенству
, то система сводится к неравенству ![]() ,
, ![]() (мы учитываем, что по условию
(мы учитываем, что по условию ![]() ), таким образом, получаем часть области определения
), таким образом, получаем часть области определения 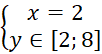 .
.
Если ![]() , то система сводится к неравенству
, то система сводится к неравенству ![]() ,
, ![]() . Учитывая, что по условию
. Учитывая, что по условию ![]() , получаем еще часть области определения
, получаем еще часть области определения 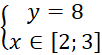 .
.
Если ![]() , то система сводится к неравенству
, то система сводится к неравенству ![]() ,
, ![]() . Учитывая, что по условию
. Учитывая, что по условию ![]() , получаем еще одну часть области определения
, получаем еще одну часть области определения 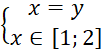 .
.
Для наглядности изобразим область определения выражения ![]() в плоскости
в плоскости ![]() (рис. 2).
(рис. 2).
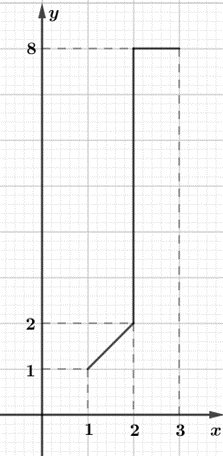
Рис. 2
Оценим значения ![]() на каждом участке:
на каждом участке:
![]()
(учитываем, что ![]() ).
).
![]()
(учитываем, что ![]() ).
).
![]()
(учитываем, что ![]() ).
).
Таким образом, наибольшее значение выражения ![]() равно 3.
равно 3.
Ответ. 3.
Задача 6. Вариант 2 (Отборочный (заочный) онлайн-этап, 10 класс, 9 баллов)
Найти наибольшее значение выражения:
![]()
при ![]() и
и ![]()
Ответ: 2.

.png&w=640&q=75)