Под итерации функций понимается результат последовательного применения суперпозиции функций: если 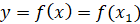 , то функции
, то функции
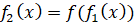 ,
, 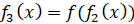 ,…,
,…, 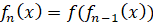
Называются соответственно второй, третьей, …, n-й итерациями функции 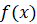 . В элементарной математике идея итерации функций помогает решать уравнения и системы уравнений, находить число решений и свойства корней уравнений.
. В элементарной математике идея итерации функций помогает решать уравнения и системы уравнений, находить число решений и свойства корней уравнений.
1. Решение уравнений
Методы решения уравнений, содержащих итерации функций, используют следующее легко доказываемое
Утверждение. Корни уравнения 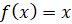 являются корнями уравнения
являются корнями уравнения
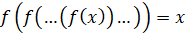
Не останавливаясь на этом пункте подробно, решим уравнение
cos8x-2cos4x-sinx=0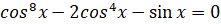
Тогда после замены
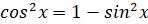 ,
,
получим
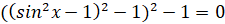 ,
,
т.е. 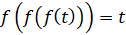 ,
,
где 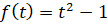 , а
, а 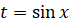 . Теперь достаточно сначала решить уравнение
. Теперь достаточно сначала решить уравнение 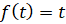 , а затем
, а затем 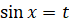 .
.
В высшей математике ставится задача вычисления предела рекуррентной последовательности, находить оценки n-го члена рекуррентной последовательности, вычислять суммы и интегралы рекуррентной последовательности.
2. Вычисление предела рекуррентной последовательности
Покажем методы вычисления пределов, использующие следующие искусственные преобразования.
Пример 1. Последовательность 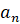 определена рекуррентным соотношением
определена рекуррентным соотношением 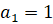 ,
, 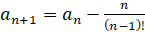 . Вычислить
. Вычислить 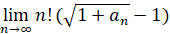 .
.
Имеем
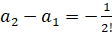 ,
, 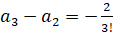 ,…,
,…, 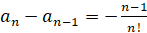 .
.
После сложения всех этих равенств, получим
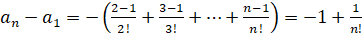 ,
,
т.е. 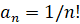 . Тогда
. Тогда
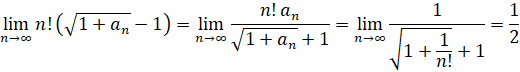
Пример 2. Рекуррентная последовательность задана условиями:
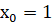 ,
, 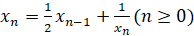 .
.
Доказать, что 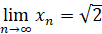 .
.
Покажем, что 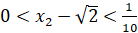 . Действительно,
. Действительно,
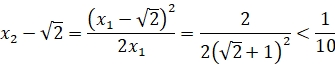
и больше 0. Аналогично доказывается, что
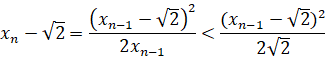
Поэтому, если на (n-1)-м шаге степень 10 была 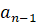 , а степень числа
, а степень числа 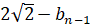 , то на n-м шаге
, то на n-м шаге 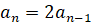 ,
, 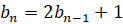 . Если положить
. Если положить
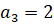 ,
, 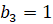 , то
, то 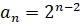 ,
, 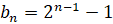 .
.
Таким образом,
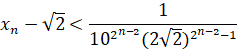
и отсюда непосредственно следует, что 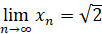 . Более того, этот подход даёт оценку разности
. Более того, этот подход даёт оценку разности 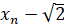 : из последнего неравенства следует, что
: из последнего неравенства следует, что
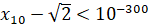 .
.
3. Оценка n-го члена рекуррентной последовательности
Пример 3. Оценить сотый член последовательности, заданной условием: 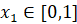 ,
, 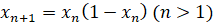
Несложно показать, что
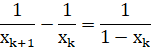
После сложения этих равенств по k от 1 до n получим
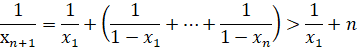
т.к. каждая дробь больше 1 при 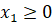 . Тогда
. Тогда
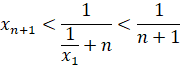
при 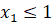 , откуда следует, что
, откуда следует, что 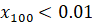
Пример 4. Последовательность an задана 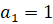 и условием
и условием
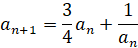
Доказать, что 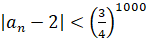 .
.
1. Можно доказать, что последовательность возрастает и ограничена, т.е. имеет предел, который находится из уравнения 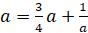 , откуда a=2.
, откуда a=2.
2. Если 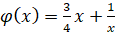 , то
, то 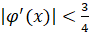 и
и 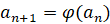 .
.
Докажем основное неравенство
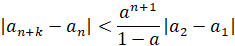
Для этого оценим разности рекуррентной последовательности 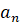 :
:
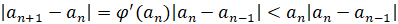
где
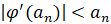 ,
,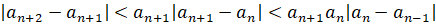 ,
,
…, 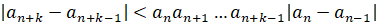 .
.
Тогда
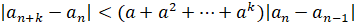
т.к. 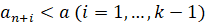 . Заменив, наконец, модуль в правой части последнего равенства и сумму степеней, получаем требуемое неравенство
. Заменив, наконец, модуль в правой части последнего равенства и сумму степеней, получаем требуемое неравенство
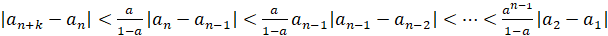 ,
,
Из которого следует, что при 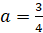 ,
,
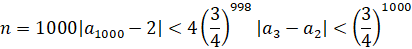
4. Вычисление сумм, содержащих рекуррентные последовательности
Пример 5. Найти 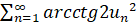 , где
, где 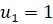 ,
, 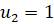 ,
, 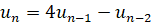 , (Городская олимпиада СПБ.,2003 г.).
, (Городская олимпиада СПБ.,2003 г.).
Вычислим значения 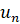 ,
, 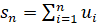 ,
, 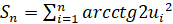 при
при 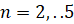
|
n |
2 |
3 |
4 |
5 |
|
|
1 |
3 |
11 |
41 |
|
|
1 |
4 |
15 |
56 |
|
|
|
|
|
|
Здесь
 ,
, 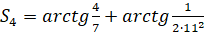 .
.
Теперь можно сделать индукционное предположение, что
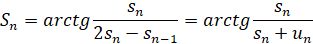
Докажем его для n+1: складывая равенства
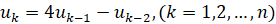
получим 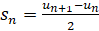 , тогда
, тогда
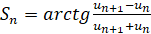 ,
, 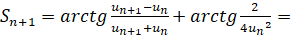
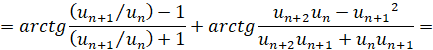
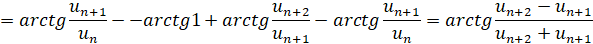
В процессе доказательства пользовались несложно устанавливаемым соотношением 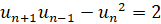 .
.
Перейдем к вычислению суммы ряда 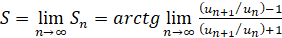 .
.
Но 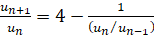 , обозначая далее
, обозначая далее 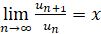 , получаем
, получаем
Уравнение 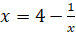 для вычисления x, которое оказывается равным
для вычисления x, которое оказывается равным 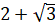 .
.
Следовательно 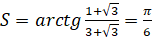 , поэтому вся сумма, начиная с n=1, будет равна
, поэтому вся сумма, начиная с n=1, будет равна 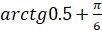 .
.

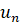
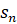
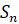
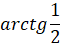
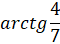
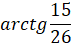
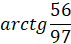
.png&w=640&q=75)