Отыскание асимптот в проективной плоскости

Данная работа посвящена исследованию методов отыскания асимптот плоских алгебраических кривых. Если кривая задана явным уравнением 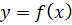, то асимптоты кривой совпадают с асимптотами графика функции, определяющей эту кривую. В этом случае всем известно, как найти эти асимптоты. Если кривая определена уравнением 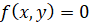, где 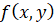 – многочлен степени n c действительными коэффициентами, то уравнения асимптот можно найти, получив параметрическое задание кривой [1, с.35]:

    (1)

В этом случае прямая y=kx+b будет асимптотой кривой при t→t₀, если существуют и конечны пределы 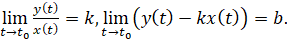Также прямая x=a является вертикальной асимптотой кривой при t→t₀, есл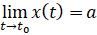и  и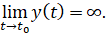  

Используя этот метод, найдены асимптоты кривых (в скобках указаны уравнения асимптот):

1. , ;
2. , ;
3. , .

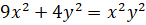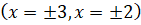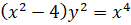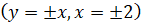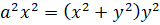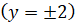Следует, однако, заметить, что переход к параметрическому заданию кривой является часто непростой задачей. В связи с этим в учебнике [2, с.69-71] предлагается метод отыскания асимптот кривой

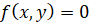,    (2)

заданной многочленом степени n c действительными коэффициентами вида

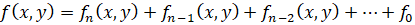,    (3)

где 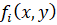– однородные многочлены степени i, но лишь при условии, что уравнение 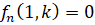имеет действительные корни кратности 1. Также в этом учебнике доказывается следующая теорема (см. [2, с.67-68]):

Если касательная к кривой (1) стремится к предельному положению, когда точка касания стремится по кривой в бесконечность, то это предельное положение есть асимптота.

Эта теорема привела к мысли пополнить евклидову плоскость R², на которой рассматриваются кривые, бесконечно удаленной прямой. Каждая точка этой прямой будет общей точкой всех параллельных прямых заданного направления, то есть центром некоторого пучка параллельных прямых. Как известно, евклидова плоскость, пополненная бесконечно удаленной прямой, называется проективной.

Переход к проективной плоскости и теорема, сформулированная выше, позволяют определить асимптоту кривой как касательную в ее бесконечно удаленной точке.

Поскольку нам придется писать уравнения прямых не только на евклидовой плоскости, но и на проективной, то напомним, как связаны евклидовы координаты точки с проективными координатами этой же точки. Если 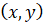– евклидовы координаты точки M, а  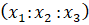– проективные или однородные координаты этой же точки, то 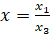, , 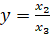где 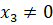. Заметим, что проективные координаты точки не могут быть равны одновременно нулю и определяются с точностью до пропорциональности, то есть, если 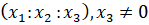 – координаты некоторой точки, то при любом α≠0 набор чисел 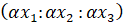является координатами той же точки. Уравнение x₃=0 является уравнением бесконечно удаленной прямой на расширенной (проективной) плоскости.

Далее, если ax+by+c=0 – уравнение прямой на евклидовой плоскости, то уравнение этой прямой на расширенной плоскости будет иметь вид .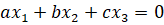

Уравнение кривой, заданной многочленом

 

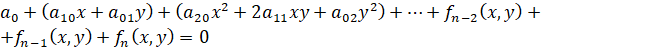
которое в проектированных координатах  будет иметь вид:

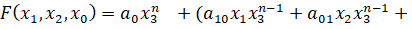
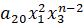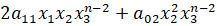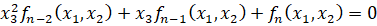  + ) +...     (4)

Уравнение касательной в точке 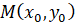, принадлежащей кривой, заданной на евклидовой плоскости уравнением (2) 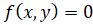, имеет вид

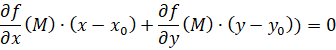    (5)

Уравнение касательной к кривой (4) в точке 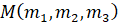этой кривой записывается следующим образом

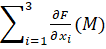
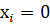 .     (6)

Формулы (5) и (6) теряют смысл, если все частные производные равны нулю.

Точка M (x,y) на кривой (2) называется особой точкой кратности k, если все частные производные до порядка k-1 от многочлена 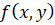 обращаются в этой точке в 0, но существует хотя бы одна производная k-ого порядка не равная 0 в ней.

В особой точке касательной к кривой в том смысле, в котором она определена выше формулами (5) и (6), не существует.

Чтобы понять, как получить уравнение касательной к кривой в ее особой точке 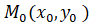 , предположим, что  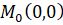и разложим многочлен  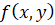степени n в ряд Тейлора в окрестности точки этой точки:

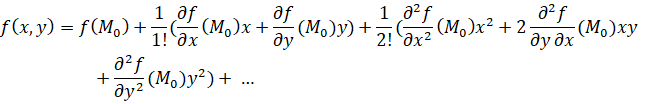
Так как 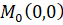лежит на кривой 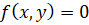, то 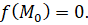Так как  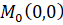– особая точка, то 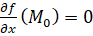, , 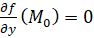и всякая прямая y=kx, проходящая через M₀, пересекает кривую в этой точке по крайней мере 2 раза. Это следует из того, что система

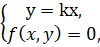
которая равносильна системе

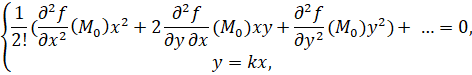
имеет по крайней мере двукратный корень x²=0 (при ∀k). Если кратность особой точки равна двум, то найдутся прямые, которые пересекаются с кривой в начале координат не два, а 3 раза. Угловые коэффициенты k этих прямых определяются из уравнения:

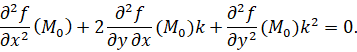
Относительно k это уравнение имеет 2 корня: различных или совпавших, а может быть и комплексных. Поэтому будем иметь 2 прямые, имеющие с кривой в точке 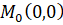 трехкратное пересечение. Эти прямые называют касательными к кривой в особой точке кратности 2. Если кривая имеет особую точку кратности 3, то в ней существуют 3 касательные, среди которых могут быть и совпавшие.

Перейдем теперь непосредственно к отысканию асимптот плоских алгебраических кривых. Остановимся лишь на методе, основанном на переходе к проективной плоскости и, соответственно, проективному замыканию кривой .

Асимптота плоской алгебраической кривой как предельное положение касательной

В данной части работы используется понятие асимптоты кривой, которое использует расширение евклидовой плоскости до проективной.

Определение. Касательная к кривой в её несобственной точке называется асимптотой этой кривой.

Задача 1. Найти асимптоты кривой, используя определение:

.

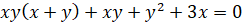Решение. Запишем уравнение в однородных координатах. Так как 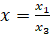, , 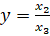то заданное уравнение перепишется в виде

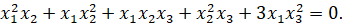
Несобственная (бесконечно удалённая прямая) x₃=0 пересекает эту кривую в трех точках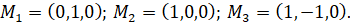

Напишем уравнение касательной в каждой из этих точек. Уравнение касательной к кривой 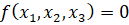  в точке  M₁ этой кривой имеет вид

.

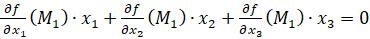Для заданной кривой ,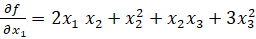

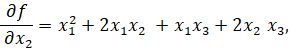
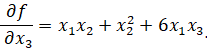
1) =

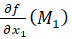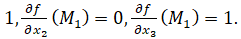
Поэтому уравнение касательной к расширенной кривой в ее точке 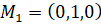имеет вид  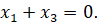Переход к евклидовым координатам дает уравнение асимптоты к данной кривой: x+1=0.

2) =

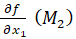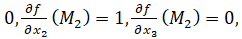
Уравнение касательной к расширенной кривой в ее точке M₂=1,0,0 имеет вид x₂=0. Переход к евклидовым координатам дает уравнение асимптоты к данной кривой: y=0.

3)

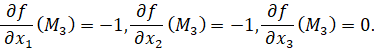
Уравнение касательной к расширенной кривой в ее точке 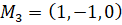имеет вид x₁+x₂=0. Переход к евклидовым координата дает уравнение асимптоты к данной кривой: x+y=0.

Ответ. Асимптоты: x+1=0, y=0, x+y=0.

Применение рассуждений, которые использовались при решении задачи, в общем случае, то есть для уравнения кривой

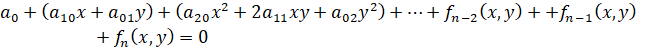
приводит к доказательству следующей теоремы.

Теорема. Пусть γ – кривая, заданная уравнением

.

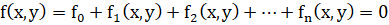Тогда:

1. Если 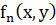  приводим и содержит сомножитель (ax+by), то есть 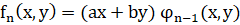, то γ имеет асимптоту с уравнением:

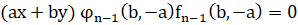     (7)

2) Если 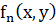 приводим и (ax+by)  является для  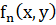множителем кратности 2, то есть

,

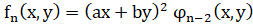и 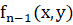 тоже имеет множитель (ax+by), но однократный, то есть

,

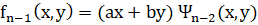то γ имеет 2 параллельные асимптоты, уравнения которых определяются из равенства

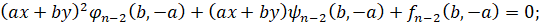    (8)

3) Если 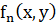приводим и (ax+by) является для  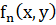множителем кратности 2, a  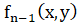не содержит (ax+by) в качестве простого множителя, то асимптот в направлении прямой ax+by=0 нет.

Доказательство. Запишем уравнение кривой в однородных координатах:

.

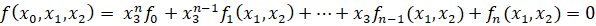Так как во всех трех случаях 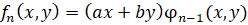, то в однородных координатах

.

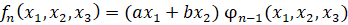Среди точек пересечения кривой с бесконечно удаленной прямой x3=0 имеется точка 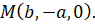 Итак, 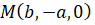 является несобственной точкой кривой. Напишем уравнение касательной к γ в точке .

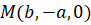Рассмотрим случай 1. В этом случае

 

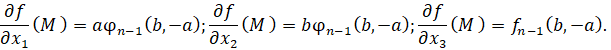
Поэтому уравнение касательной к γ в точке M(b,-a,0)  запишется следующим образом

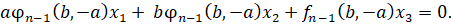
Переход к евклидовым координатам: 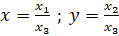дает уравнение асимптоты кривой γ.

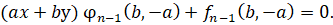
Случай 2. В этом случае 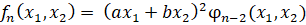 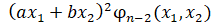   , а в разложении  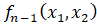на множители множителя 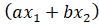нет.

Тогда значения частных производных в точке 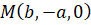 соответственно равны

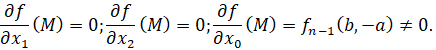
Это значит, что в этом случае 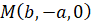 особой точкой не является, и уравнение касательной в ней к кривой на расширенной плоскости имеет вид x₃=0 . То есть касательная – это несобственная прямая. Поэтому кривая в евклидовой плоскости асимптот не имеет.

Таким образом доказана теорема, позволяющая не только определять наличие асимптот у плоской алгебраической кривой, расположенной в евклидовой плоскости, но и дающая алгоритм написания уравнения асимптот, если они существуют.